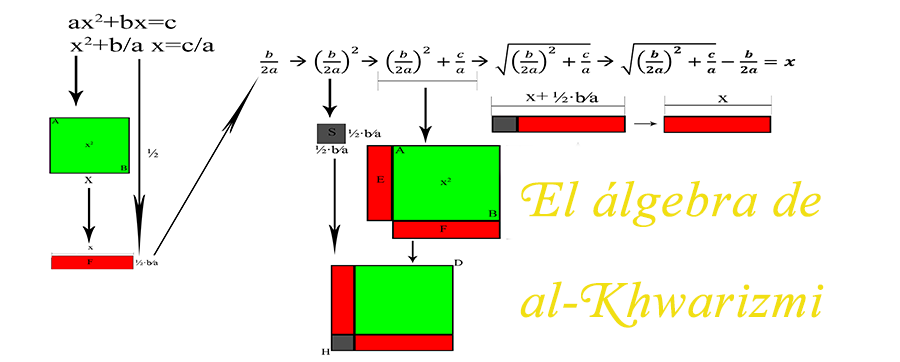
El álgebra de al-Khwarizmi
Cuando se dice que los árabes trajeron las matemáticas a Europa (a España, al menos), se hace referencia, principalmente, a lo que recoge al-Khwarizmi en una de sus obras fundamentales, Compendio de cálculo por reintegración y comparación (وَالْمُقَابَلَةالْكِتَابْ الْمُخْتَصَرْ فِيْ حِسَابْ الْجَبْرْ ), en la que se asientan las bases del álgebra. Esta disciplina existía desde mucho antes, tanto en textos babilónicos como indios, pero la magnitud, claridad y el impacto de esta obra permiten justificar el origen del álgebra en ella (al menos a nivel práctico).
Es este un libro de herencia más hindú que griega, aunque más racional y menos dogmático que sus antecesores guptas, muy centrado en ejemplos y con una gran función didáctica. Muchas de las ideas de este tratado son similares a las de los Elementos de Euclides, pero planteadas en base numérica (algebraica), no meramente proporcional (geométrica). El primero nunca diría (o nunca dijo) que el área de un cuadrado más el de un rectángulo es igual a 30, o a 25, sino al doble de esta o aquella figura. Al-Khwarizmi, por el contrario, se centra en la magnitud, en el dato numérico (hasta el punto de que la mayor parte del texto son casos concretos), hecho de vital trascendencia para las matemáticas. Incluso el libro comienza asentando las bases del álgebra mediante la referencia a la importancia del número.
«Cuando pienso qué quiere la gente generalmente cuando se habla de cálculo, concluyo que es siempre un número. También he observado que cada número está compuesto de unidades y que cualquier número puede ser dividido en unidades» (al-Khwarizmi: 5).
Así, además de tratar los problemas matemáticos de manera más concreta y material, hace las matemáticas más fáciles de usar, aunque menos puras, quizás menos útiles para el pensamiento, pero más para la administración. No es casual, sino causal, que esta obra se escribiese a petición del califa al-Mamún con una función didáctica y un claro carácter utilitario, que tienen que ver con las herencias o la división de tierras. Además, al dar soluciones universales a determinados tipos de ecuaciones, incluso con pasos para llegar de forma segura a la conclusión, hace que este libro parezca un manual de instrucciones con una clara función utilitaria, como se dice explícitamente en la introducción:
«[busco] aquello que los hombres constantemente necesitan en casos de herencia, legados, divisiones, juicios y comercio, y en todos sus negocios con los demás, o en la medida de la tierra, la excavación de canales, la geometría computacional y otros objetos de varios tipos» (al-Khwarizmi: 3–4).
Merece la pena mencionar que en la introducción se intuye una concepción de la ciencia que podría ser perfectamente válida un milenio después de escrita, pues se refiere a su multidisciplinariedad, a la dificultad y las penurias (intelectuales y vitales) que exigen la obtención de conocimientos, el carácter histórico y literario (es decir, codificado en libros) de la ciencia, la importancia de la corrección recíproca y continua entre expertos, incluso de distintas épocas… Respeto al contenido de esta obra, se dan en ella convenciones que todavía seguimos usando (como la multiplicación de números negativos), se plantea la que ahora llamamos «regla del tres» (que permitiría resolver «todos los cálculos de los negocios» (al-Khwarizmi: 74), entiéndanse los negocios del siglo III de la Hégira), así como fórmulas para las áreas de distintas figuras y volúmenes, y normas para la gestión de herencias. No obstante, la cuestión más importante que se aborda en este libro es la formulación, el desarrollo y la explicación de un método para resolver ecuaciones de segundo grado.
Ecuaciones de segundo grado
Las ecuaciones de segundo grado son del tipo: ax² + bx = c, es decir, relacionan dos figuras [o parcelas] (ax² y bx) y un número [o cantidad de dinero] (c), como veremos. Si nos olvidamos por un momento de las matemáticas aprendidas en la escuela, veremos lo complicado que es resolver este tipo de ecuaciones sin fórmulas ni métodos estandarizados, por mero tanteo, lo que debía ser un quebradero de cabeza para al-Mamún, y cualquier notario de la época. En cuanto los números son relativamente grandes (piénsese en una herencia media, que ya puede tener números de dos o tres cifras para operar), estas ecuaciones no se pueden resolver sin un método. Por ello al-Khwarizmi explica una forma de resolverlas, que básicamente consiste en reducir (o completar, de ahí el título de la obra) la ecuación a cuadrados unitarios, dividir el número de raíces («b») a la mitad, multiplicar la cantidad restante por sí misma, sumarle el número simple («c»), sacar la raíz cuadrada del resultado y a eso restarle el número de raíces divididas por dos. Como vemos, es un procedimiento mecánico que se puede realizar para obtener un resultado sin tomarse la molestia (ni el tiempo) de entender qué se está haciendo. Dado que todo esto se muestra con ejemplos, veamos uno desarrollado con fórmulas (aunque, curiosamente, al-Khwarizmi lo explica todo con palabras, no usando un solo número en toda la obra).
2x² + 10x = 48
Reducimos a una sola x², dividiendo todo entre dos:
x² + 5x = 24
Y aplicamos los pasos propuestos por al-Khwarizmi:
Lo cual responde a la pregunta de «¿cuál debe ser la cantidad de dos cuadrados [2x²] que, cuando se suman y se le añade diez veces su raíz [10x], da lugar a cuarenta y ocho dirhams?» (al-Khwarizmi: 9). Nótese la referencia a una divisa típica árabe, usada por el propio autor. Operando los números anteriores obtendríamos un resultado: x = 3. No obstante, es más importante (para entender lo que estamos haciendo, no para ver si podemos comprar la parcela de nuestro primo segundo), universalizar este método de tal manera que lo podamos usar en cualquier situación, algo que al-Khwarizmi tiene en mente y que expresa en varias ocasiones: este método «siempre funciona» (al-Khwarizmi: 10). Lo podríamos transcribir de la siguiente manera:
ax² + bx = c
Lo que ha pasado a popularizarse para ecuaciones reordenadas igualando a cero (ax² + bx + c = 0), de la siguiente manera (lo que se obtiene básicamente despejando la ecuación general anterior).
Pero más allá de dar un método, y aquí reside uno de los elementos más importantes de esta obra, al-Khwarizmi explica por qué hay que realizar estos pasos. Una ecuación de doble grado (por ejemplo: x² + 10x = 39) explica la relación entre un cuadrado, una raíz y un número, lo que geométricamente corresponde a una figura cuadrada (x²), un rectángulo que comparte un lado con dicho cuadrado (10x) y un número al cual se igualan (39). Podríamos decir que, si tengo dírhams suficientes para comprar treinta y nueve unidades (de, por ejemplo, metros cuadrados o hectáreas), y quiero comprarme una finca (cuadrada) en Damasco, y otro espacio para montarme un taller (10x) en las afueras, ¿qué dimensiones máximas pueden tener estos espacios?
Nótese que da igual que la segunda finca no comparta un lado x del mismo tamaño que el del cuadrado de la primera, y tampoco importa que quieras una finca cuadrada o no, pues a través de los Elementos de Euclides (que al-Khwarizmi conocía y presuponía) se pueden transformar una figura en otra (a través de la proposición 37 del libro II, por ejemplo, se convierte una figura irregular en una de un lado determinado).
Para dejarnos de líos, podríamos aplicar el método de al-Khwarizmi:
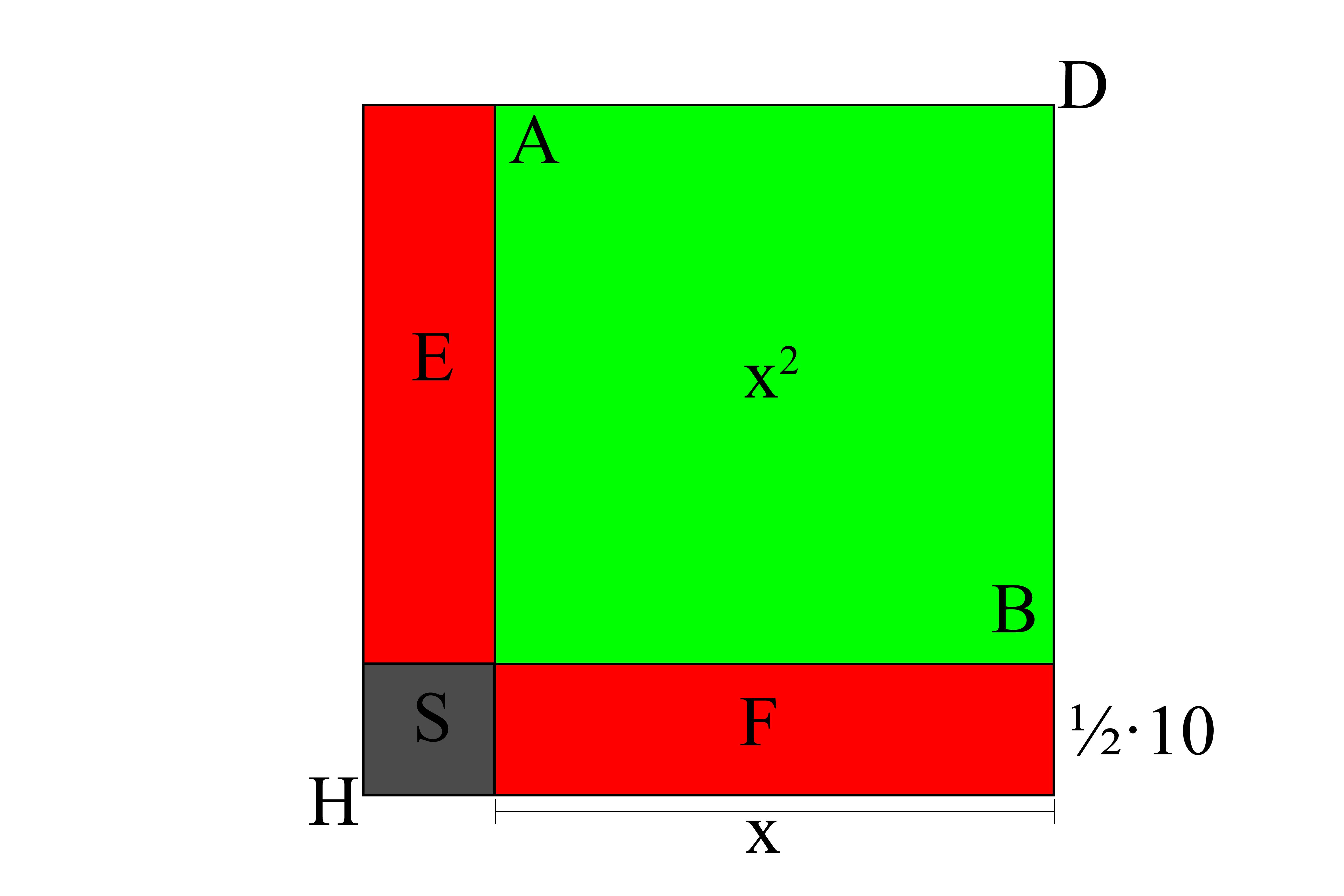
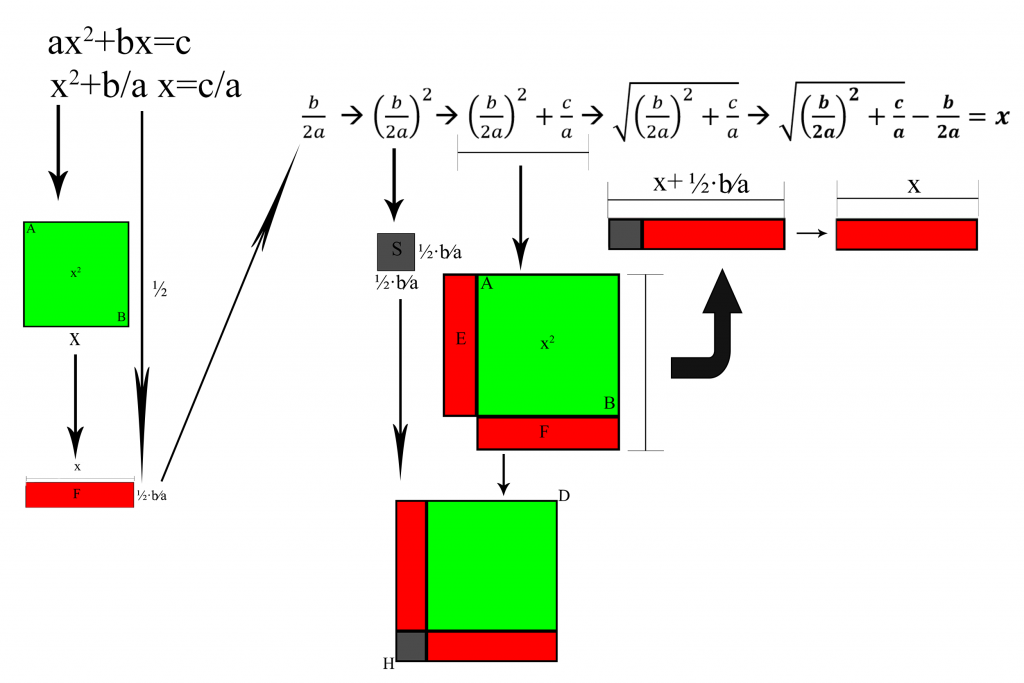
Es decir, podría comprarme una parcela de nueve metros cuadrados y otra rectangular de diez por tres (un poco justo, quizás). Pero, para entender lo que está ocurriendo en este método y en la fórmula general, hay que recurrir a la geometría. Para ello dibujamos un cuadrado AB, que será x², y en dos de sus laterales añadimos dos rectángulos (llamémoslos E y F) cuya suma sea igual a 10x, lo que se puede hacer fácilmente dibujando dos paralelogramos que compartan un lado con x², que sería x, y dando al otro lado una anchura de ½·10. Así, cada uno de los paralelogramos tendría como área la mitad de 10x, siendo 10x la suma de los dos. Para completar un cuadrado que incluya estas tres figuras, quedaría una esquina cuadrada (S) de lado ½·10, por construcción.
La suma del cuadrado total (DH) sería:
Dado que sabemos que x² + 10x = 39 (por la ecuación que queremos resolver) y que S es igual a 25 (operando los números, ya que no tienen incógnitas), sacamos la superficie de DH, que serían 64. Un lado de DH, por lo tanto, mediría 8 (la raíz cuadrada de 64). Y esto tendría en cuenta x y el lado de una de las esquinas, que sería ½·10. Por lo tanto:
8 = x + ½·10
x = 8 – ½·10 = 3
Esto también lo podemos hacer para cualquier caso abstracto: x²+b/ax=c/a, que en nuestra figura sería: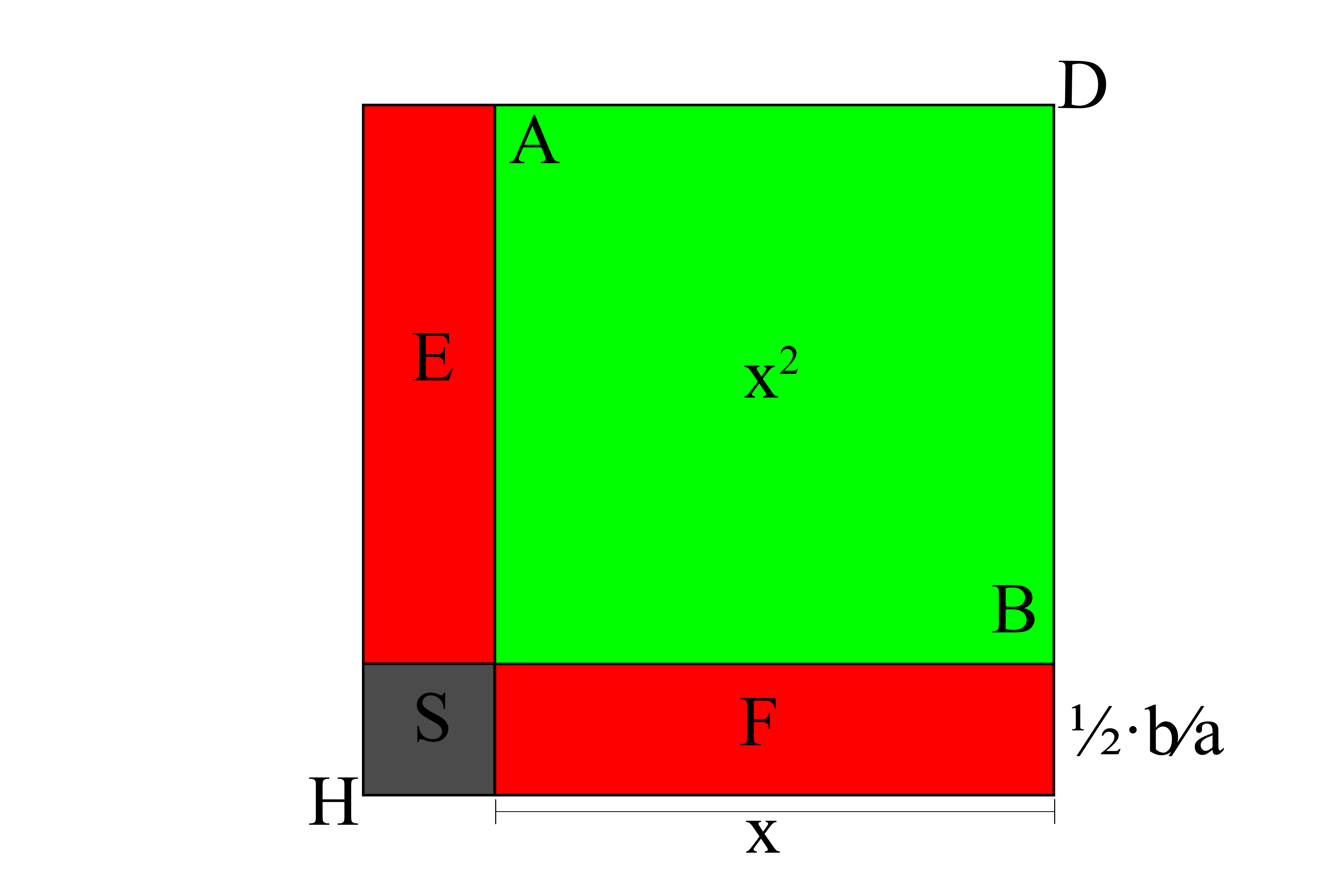
Donde DH sería:
DH = AB + E + F + S
Dado que E=F, por construcción:
Y que S es, también por construcción:
Y AB es, por definición, x², DH quedaría como:
Y, dada la ecuación que queremos solucionar:
E igual que en el caso anterior, x sería la raíz cuadrada de DH menos un lado de S, es decir:
Lo cual podemos despejar de la siguiente manera, para dar lugar a fórmula general para resolver ecuaciones de segundo grado:
Por lo tanto, con este método sacamos un lado del cuadrado x² (es decir, x), creando una figura en la que x² se suma a 10x, por construcción, al que hay que restarle una esquina que queda como subproducto. En el método directo propuesto por al-Khawarizmi (anterior a la explicación), lo que se hace es, en primer lugar, reducir el número de x² que tenemos a uno (lo que nos permitirá formar una figura cuadrada sencilla). Luego cogemos el número de x y lo dividimos entre dos, con lo que tenemos el lado del paralelogramo que queremos formar junto a x². Dado que esto sería (por construcción), en lado de la esquina cuadrada que quedaría como subproducto, elevamos lo obtenido al cuadrado para obtener su área, y sabemos que esto junto a x² + (a/b)·x es el cuadrado total que hemos construido (y dado que x² + (a/b)·x es c/a, por la ecuación que queremos resolver, sumamos este último término), lo cual al sacar la raíz cuadrada nos da un lado y, al restarle el lado de la esquina que queda como subproducto, nos da x. Y ya sabemos qué finca podemos comprarnos.
Citas: Al-Khwarizmi. The Compendious Book on Calculation by Completion and Balancing. Translation by Frederic Rosen, 1831.

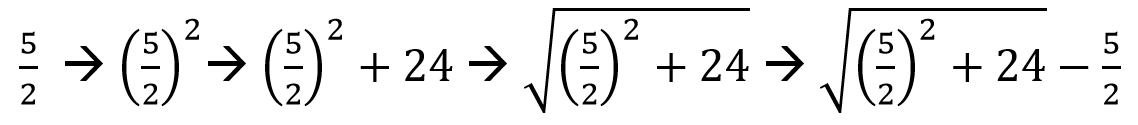
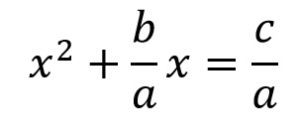
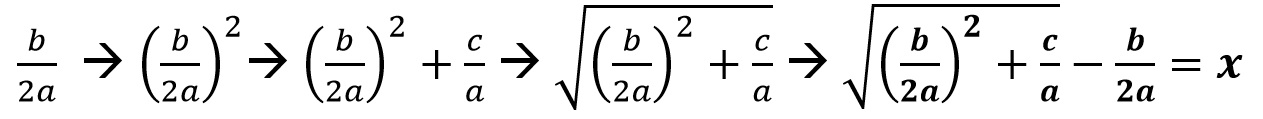
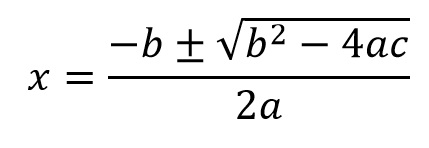
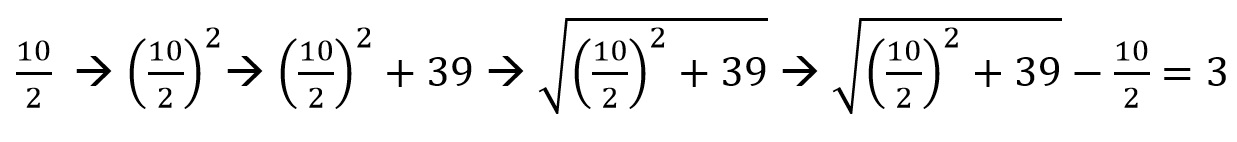
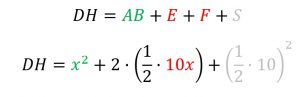
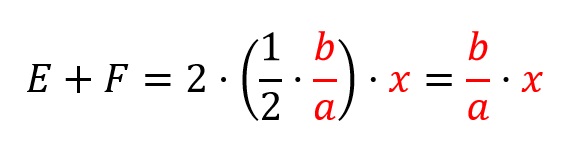
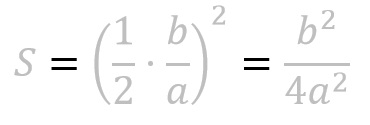
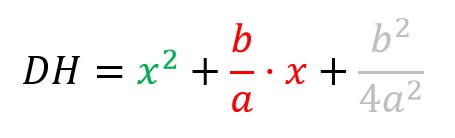
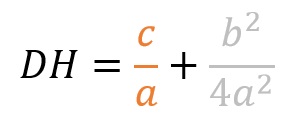
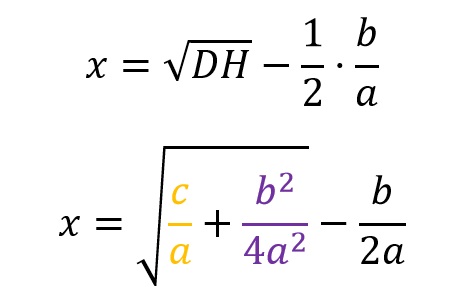
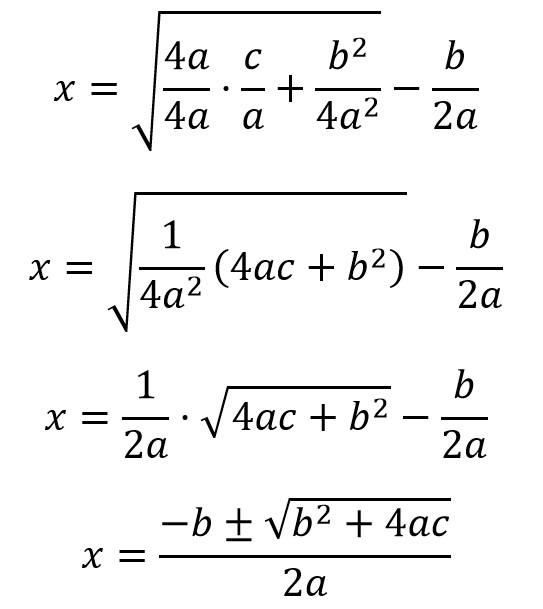
Gracias, muy bien explicado. Lo contaré en clase.
[…] El álgebra de al-Khwarizmi […]