El teorema de Pitágoras

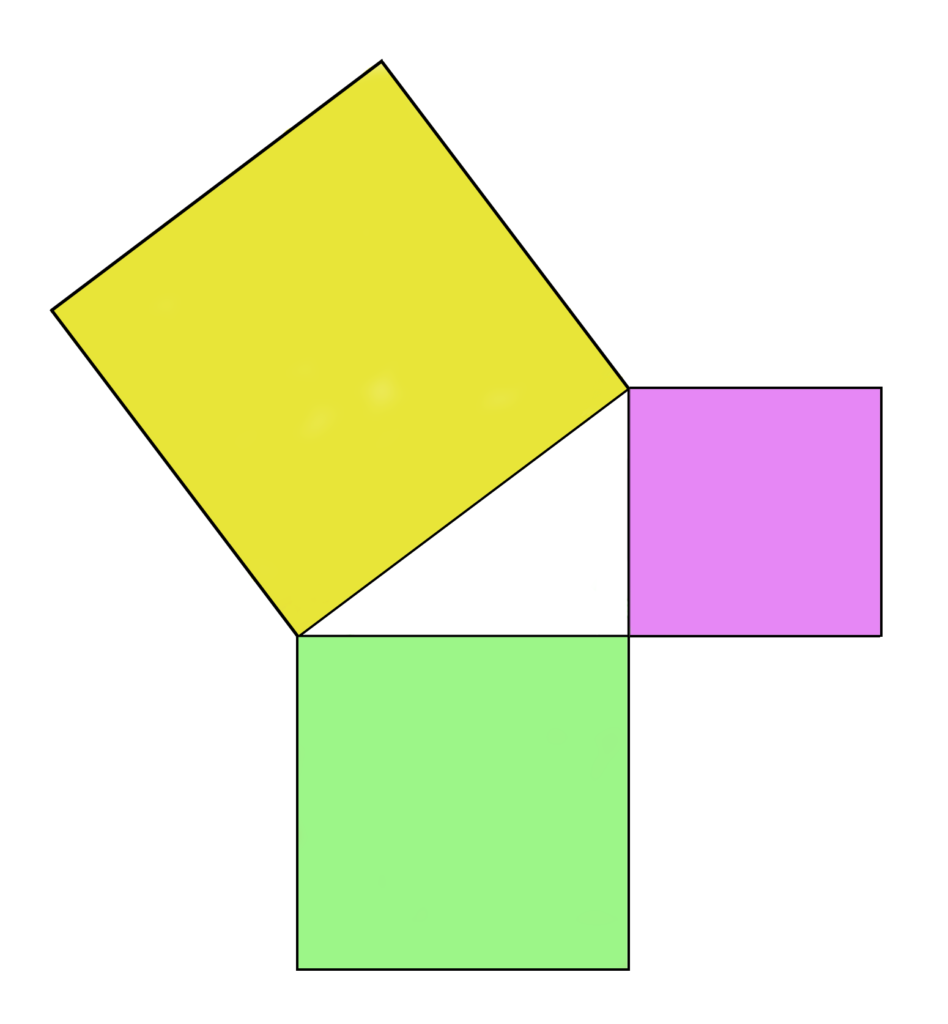
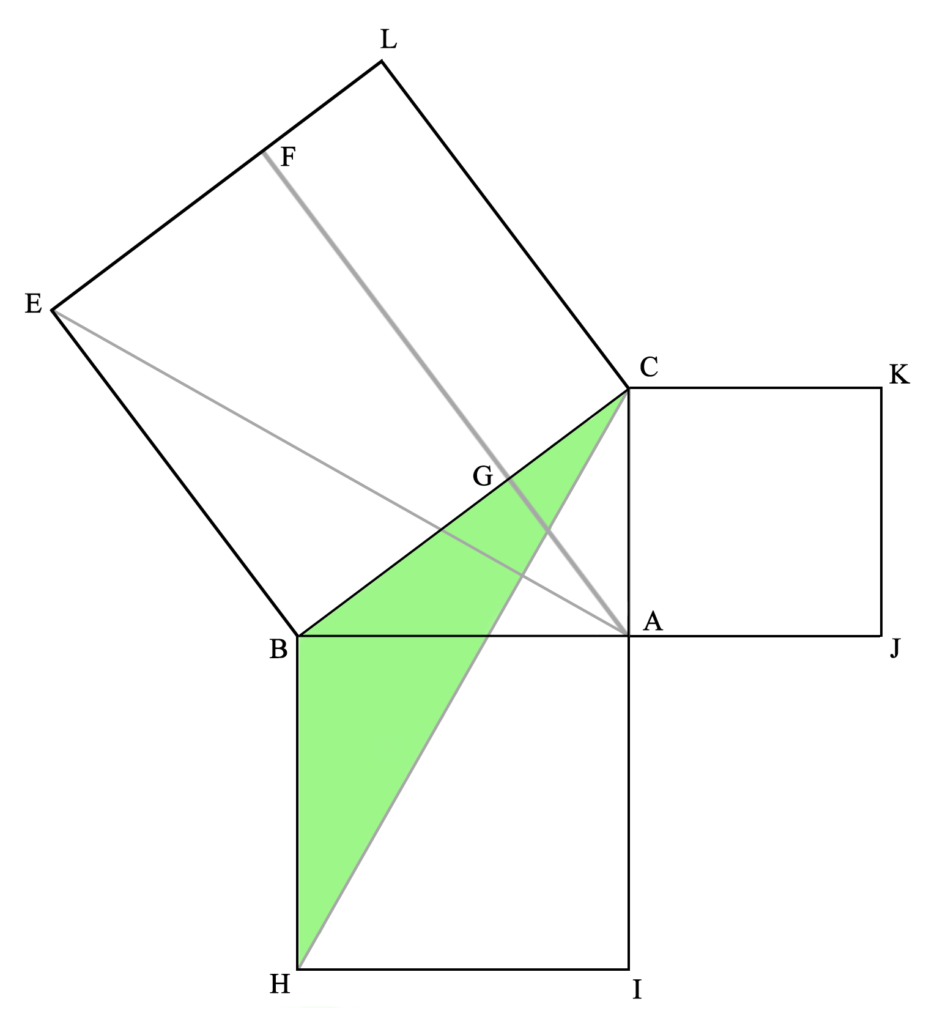
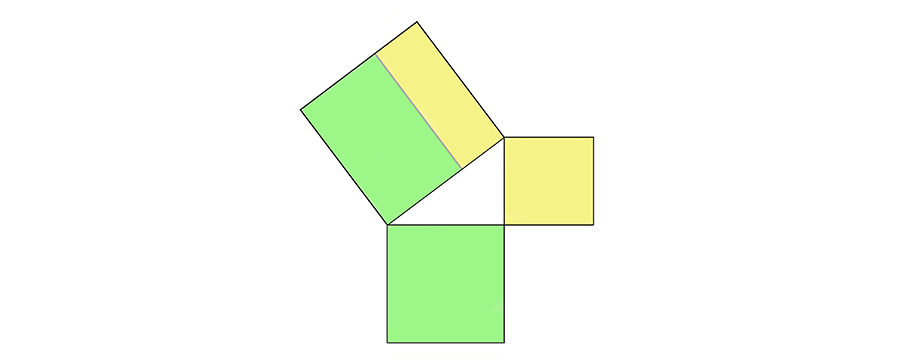
       La contribución más conocida de Pitágoras a la geometría, es el teorema que lleva su nombre, según el cual «en el triángulo rectángulo el cuadrado de la hipotenusa equivale a la suma del cuadrado de los catetos» (D12, similar en P36) o, como recoge Euclides: «en los triángulos rectángulos el cuadrado que pende del lado opuesto al ángulo recto es igual a los cuadrados formados en los lados que forman dicho ángulo» (P47L2). O, dicho de manera algebráica (que se normalizará siglos más tarde con al-Khwarizmi): a² + b² = c² lo que podemos ver en la siguiente imagen:

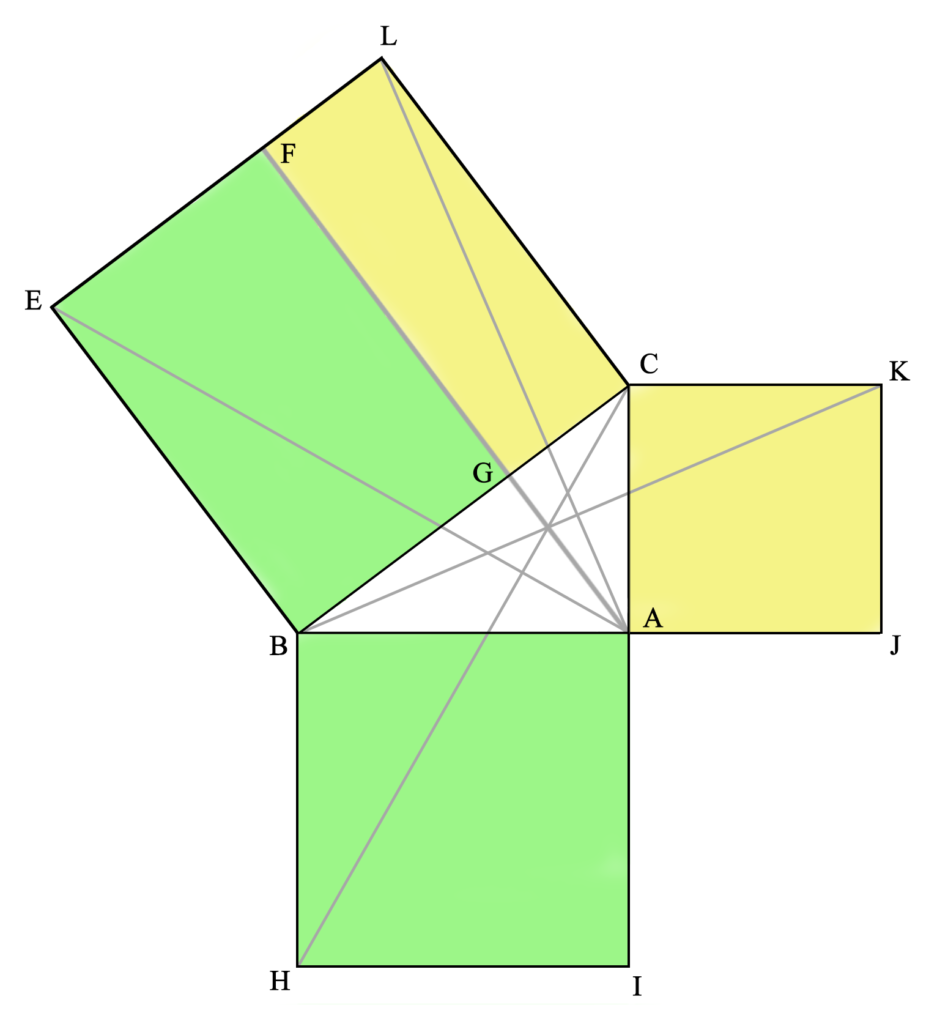
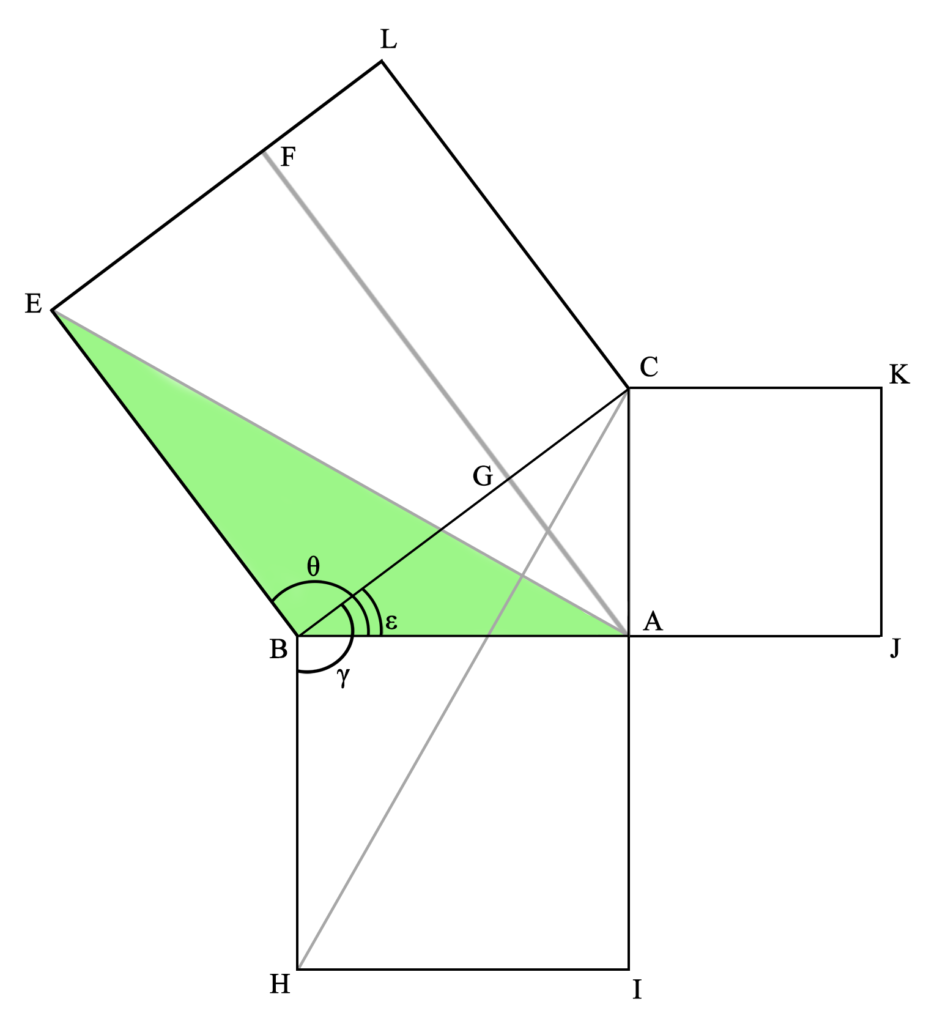
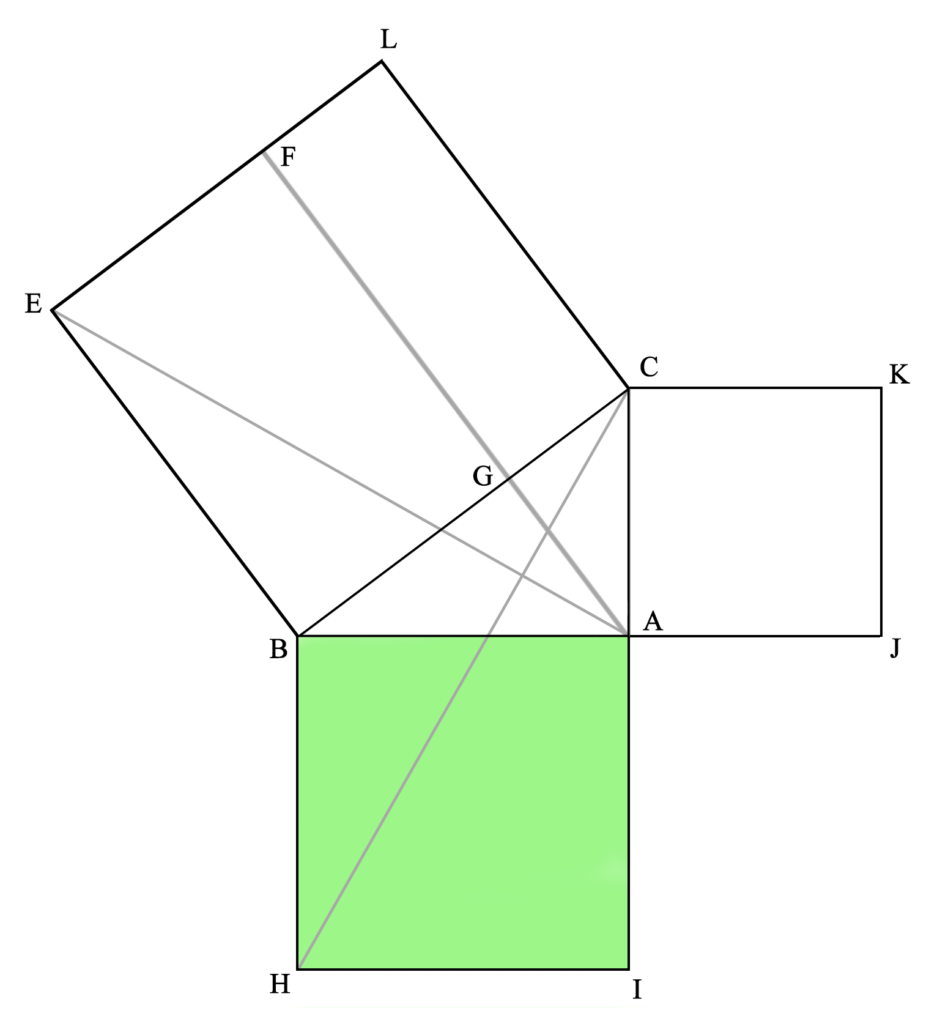
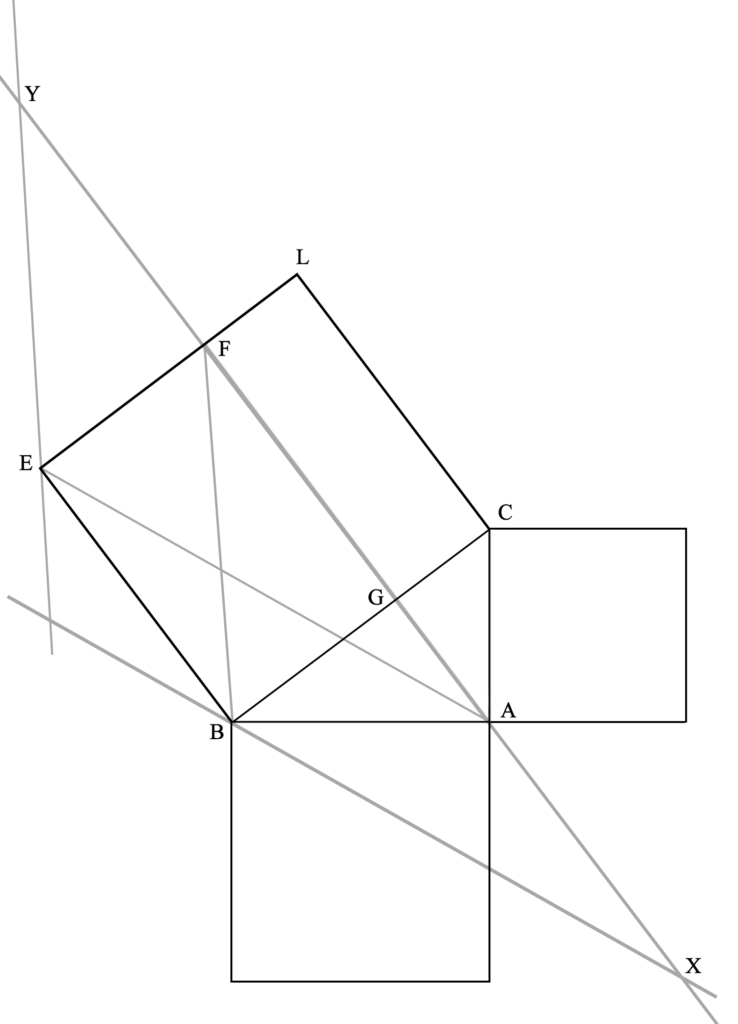
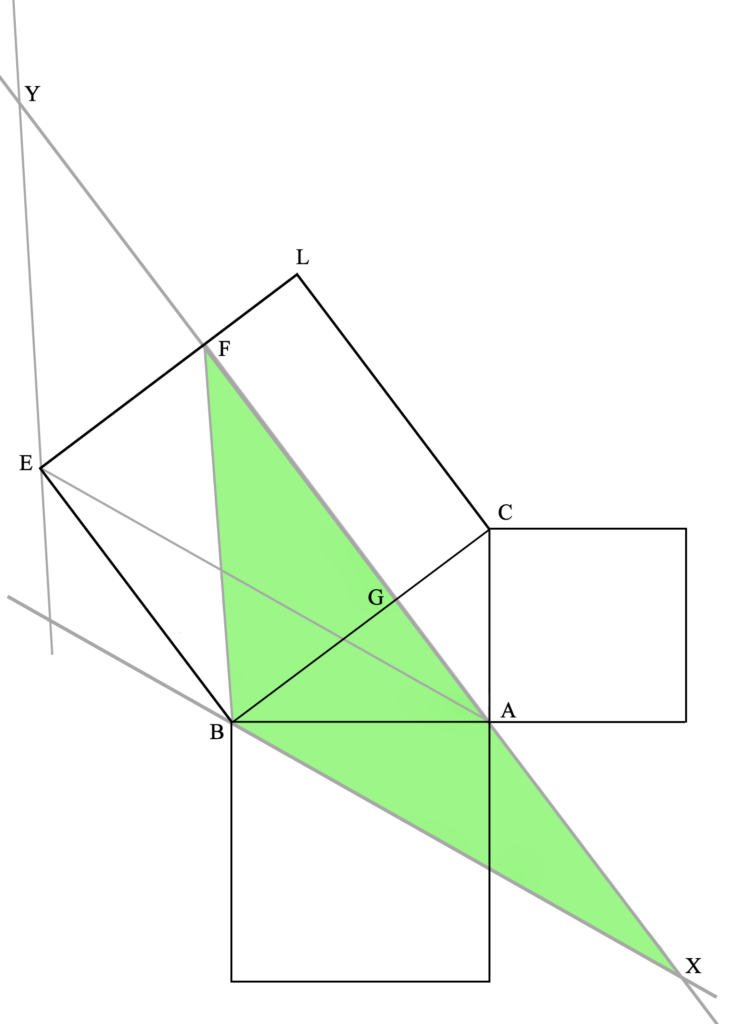
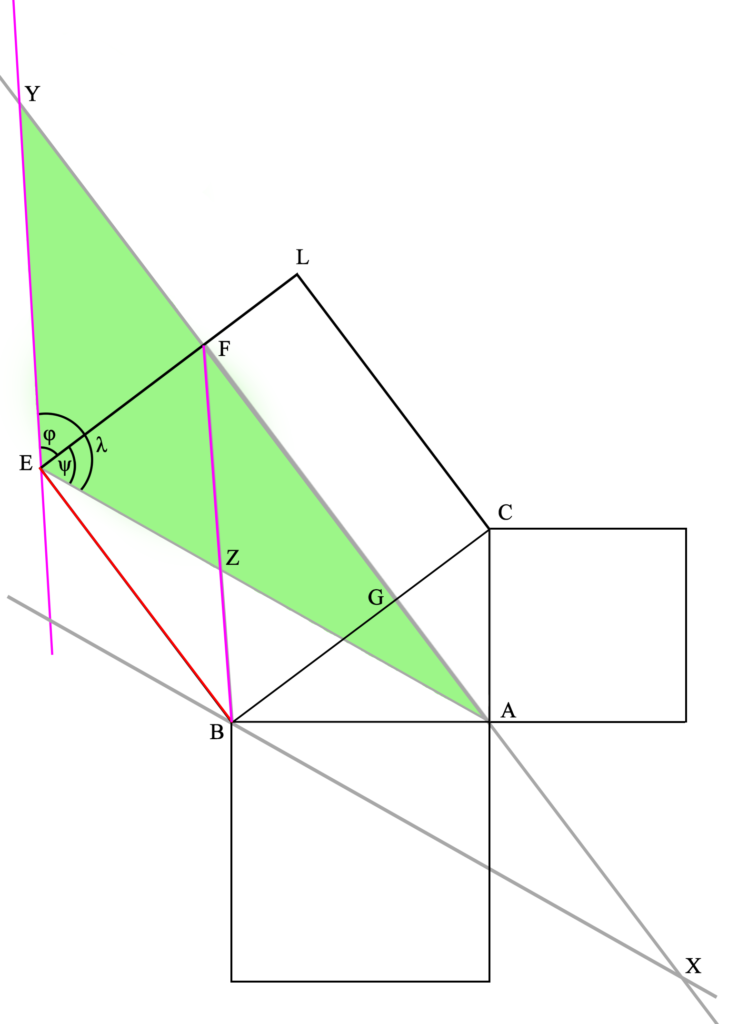
       Para demostrar esta proposición (que es el procedimiento más importante en geometría, incluso más que el planteamiento de la proposición), partimos del anterior triángulo rectángulo y los cuadrados adyacentes, y dibujamos las rectas AL, AE, CH y KB, así como la paralela a BE (y a CL) por A. Así podremos visualizar más fácilmente lo que la proposición nos dice:

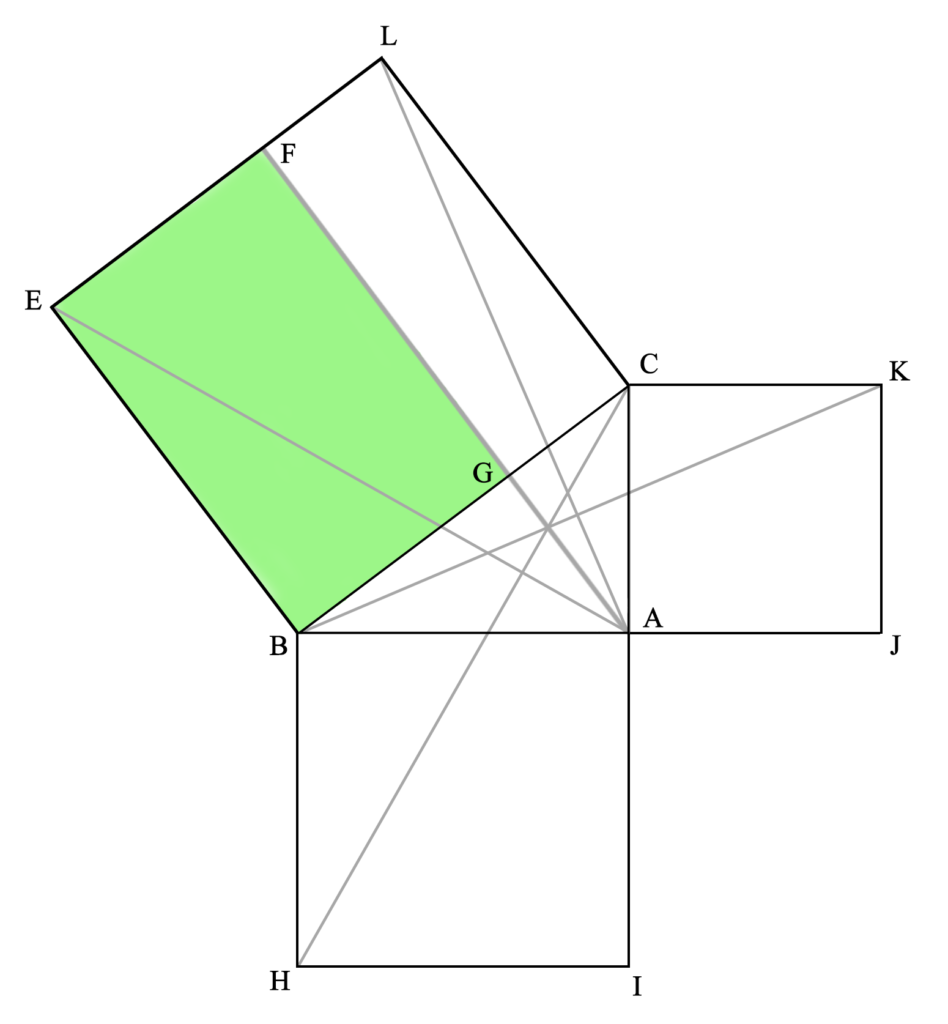
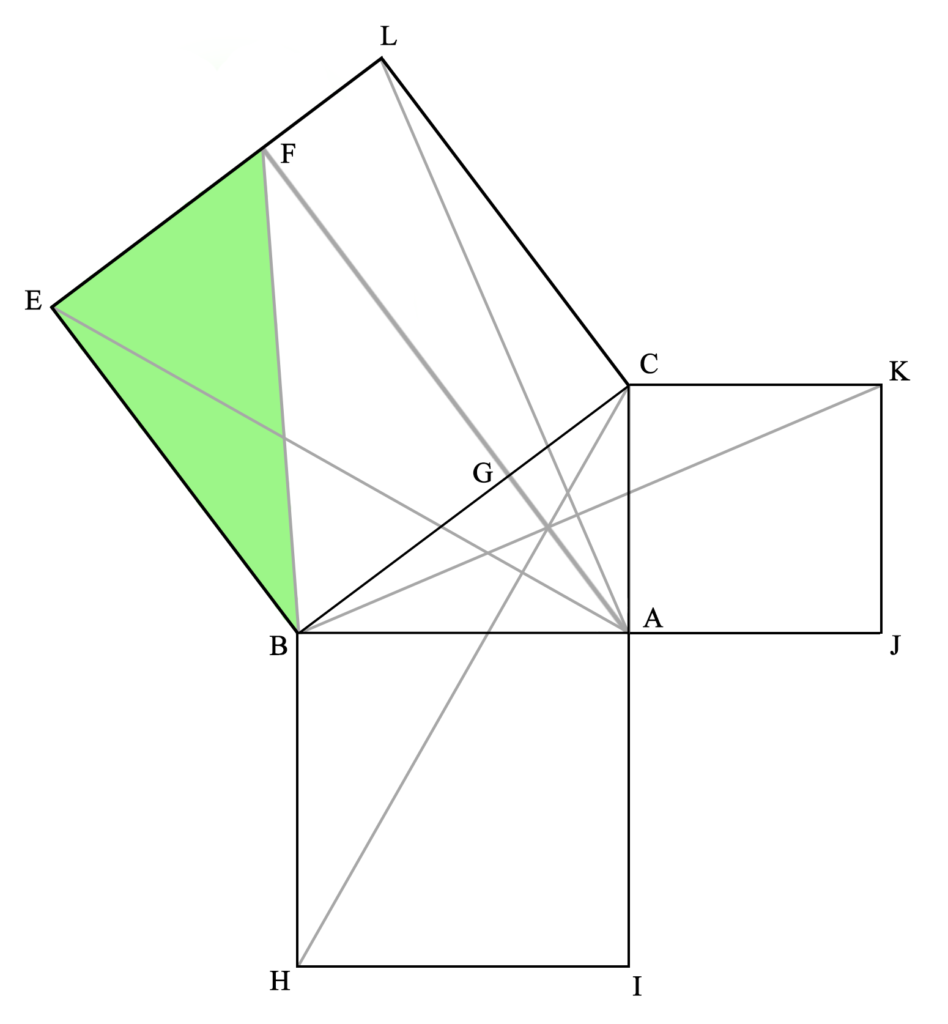
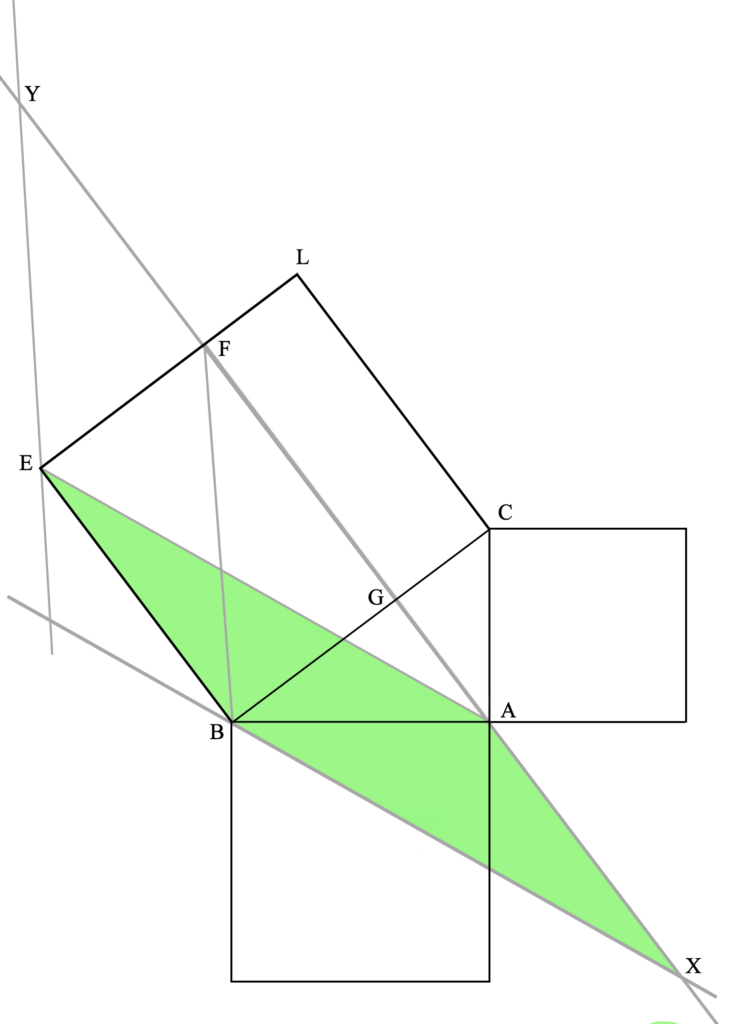
       Aquí vemos que el triángulo AEB tiene la mitad del área del cuadrilátero GFEB, ya que comparten la base BE y la altura FE (las rectas FA y EB, en las que se encuentran la base del triángulo y su vértice opuesto, así como los lados opuestos del cuadrilátero, son paralelas). Una explicación completa (geométrica) de esta igualdad la daremos más abajo.

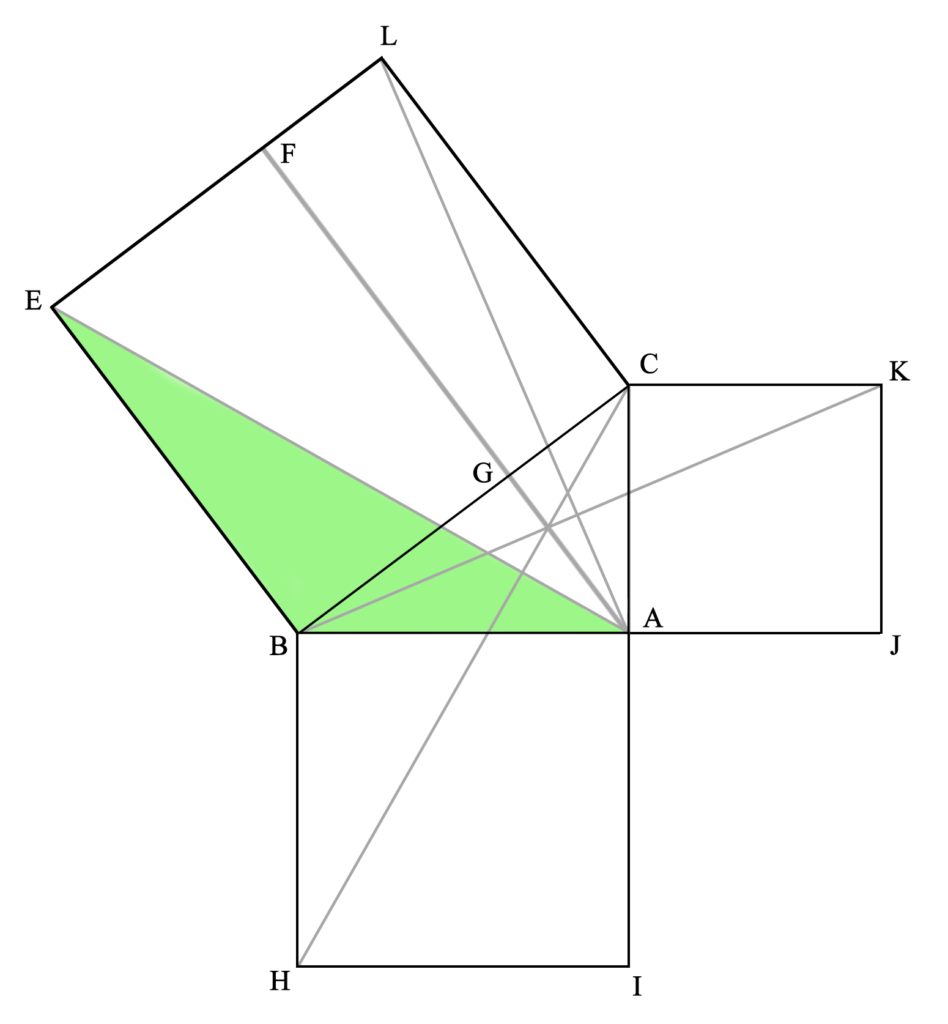
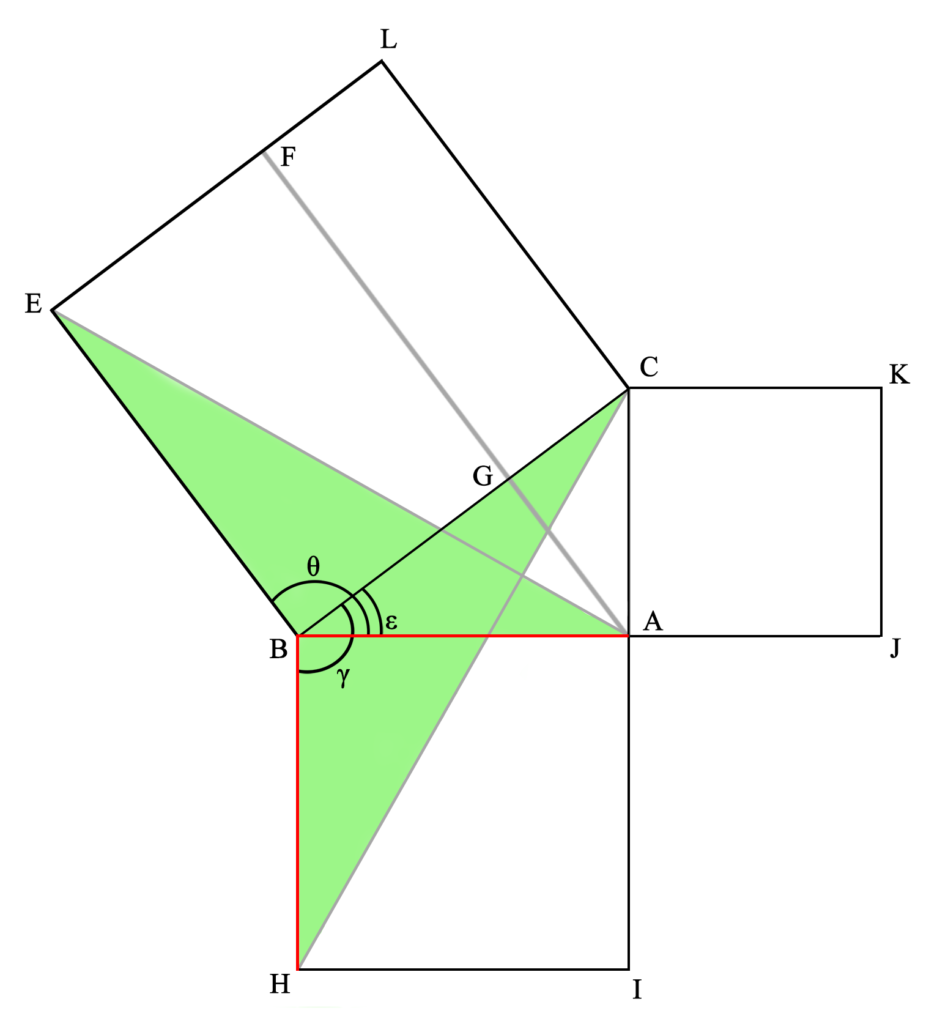
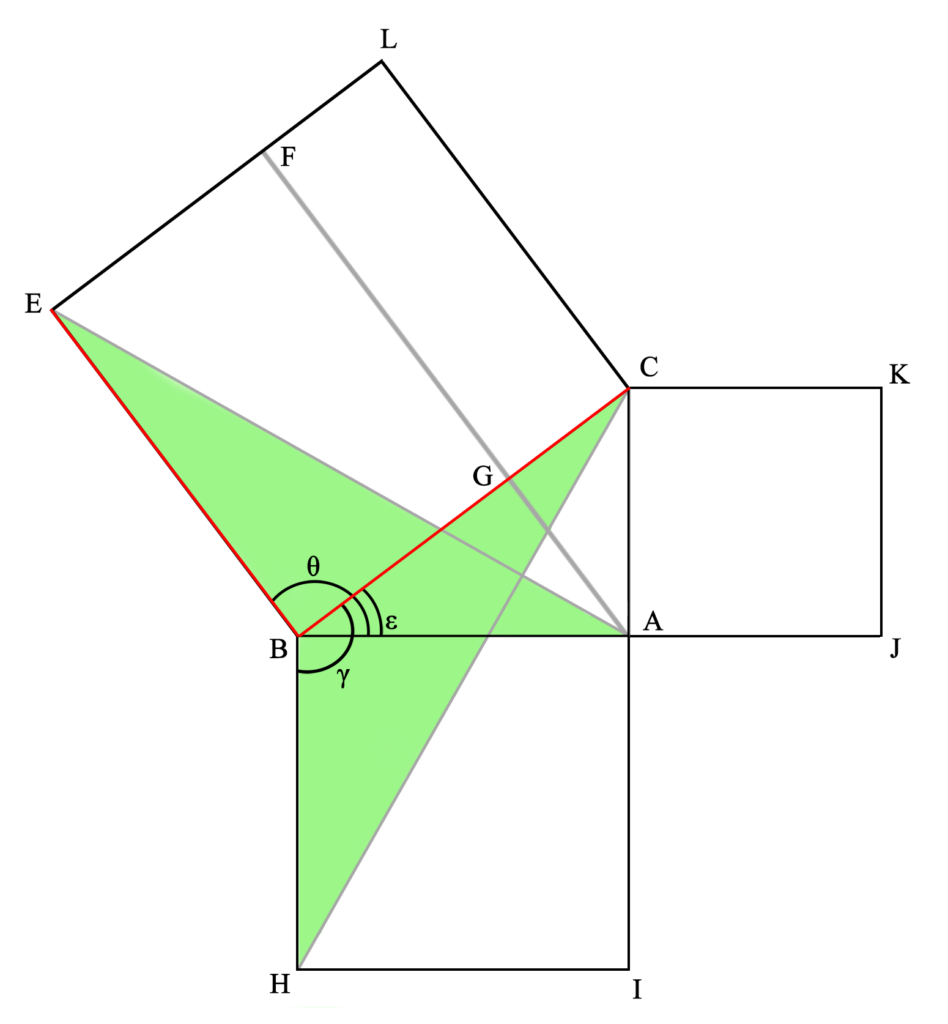
       Este triángulo AEB es idéntico al CHB.

       Esto se demuestra comprobando que ambos tienen dos lados y un ángulo iguales (demostrado por P4L1, como luego veremos), ya que el lado AB (del primer triángulo mencionado) es igual al BH (del segundo triángulo), por ser dos lados de un cuadrado (pues así lo hemos construido –téngase en cuenta que la definición de un cuadrado es aquella figura de cuatro lados iguales entre sí y paralelos dos a dos, es decir, con cuatro ángulos interiores rectos–) y el lado BE es igual al BC, por la misma razón. Además, el ángulo θ es igual al γ, ya que ambos cuentan con un ángulo recto (del cuadrado, por construcción y definición) más el ángulo ε, igual en ambos casos (permitido por noción común dos). Por lo tanto, estos triángulos son exáctamente iguales.

 

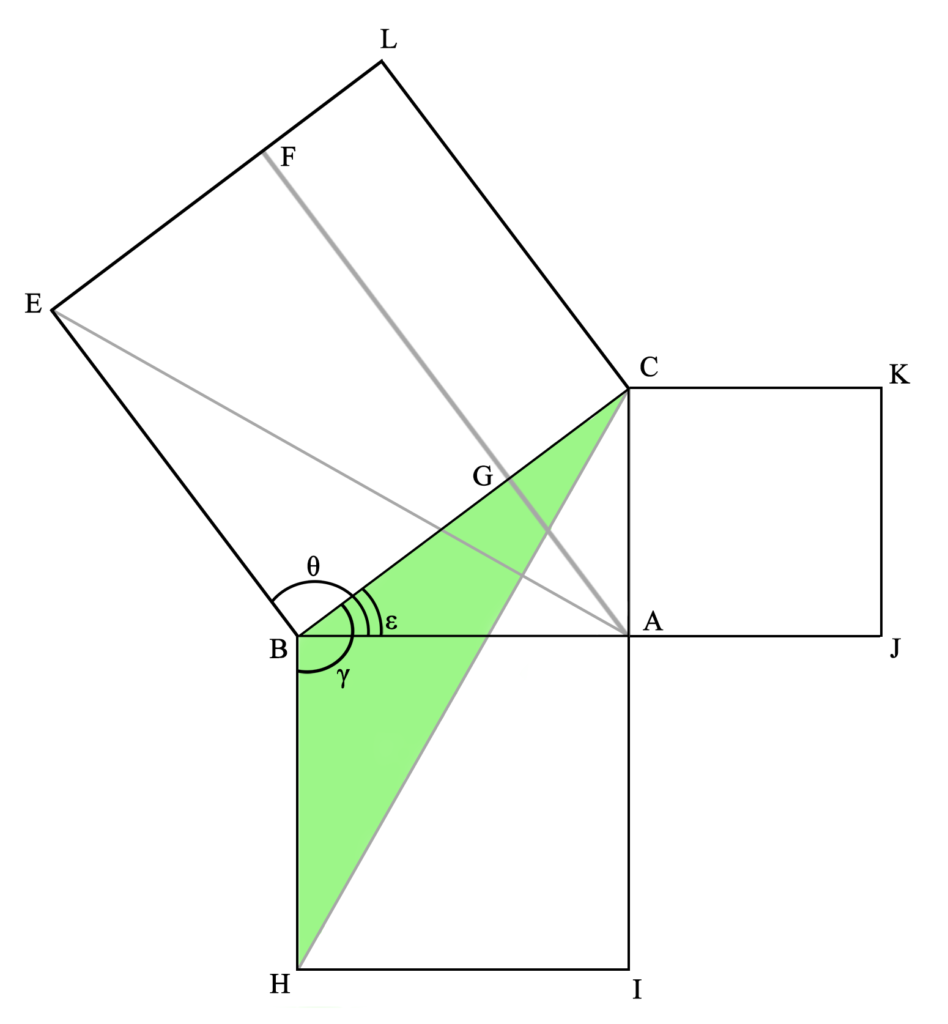
       Y, por último, el triángulo CHB es la mitad del área del cuadrado ABHI, por tener la misma base BH y la misma altura HI (las rectas BH y IC son paralelas), igual que ocurría con el triángulo AEB y el cuadrilátero GFEB.

       Por lo tanto, si el triángulo CHB es la mitad del área del cuadrado ABHI y el triángulo AEB es la mitad del cuadrilátero GFEB y ambos triángulos (CHB y AEB) son idénticos, tenemos que ambos cuadriláteros (ABHI y GFEB) tienen el mismo área (aunque no la misma forma).

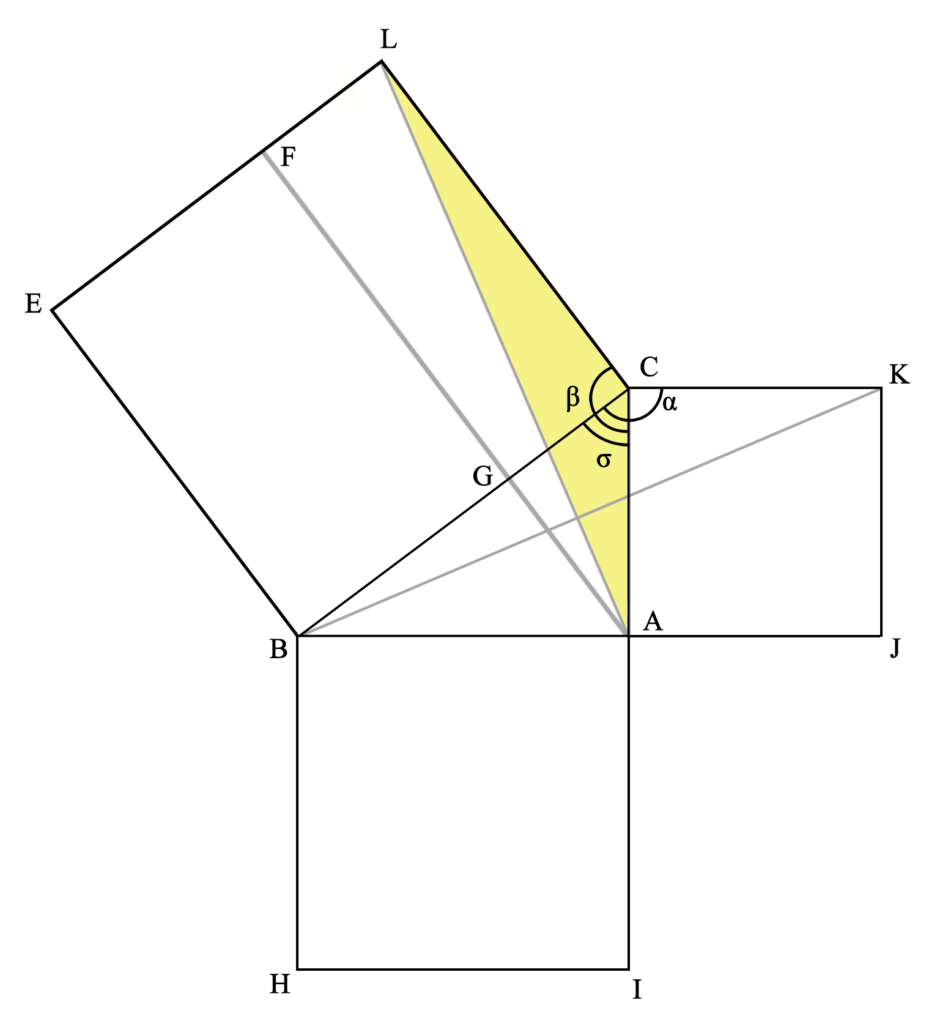
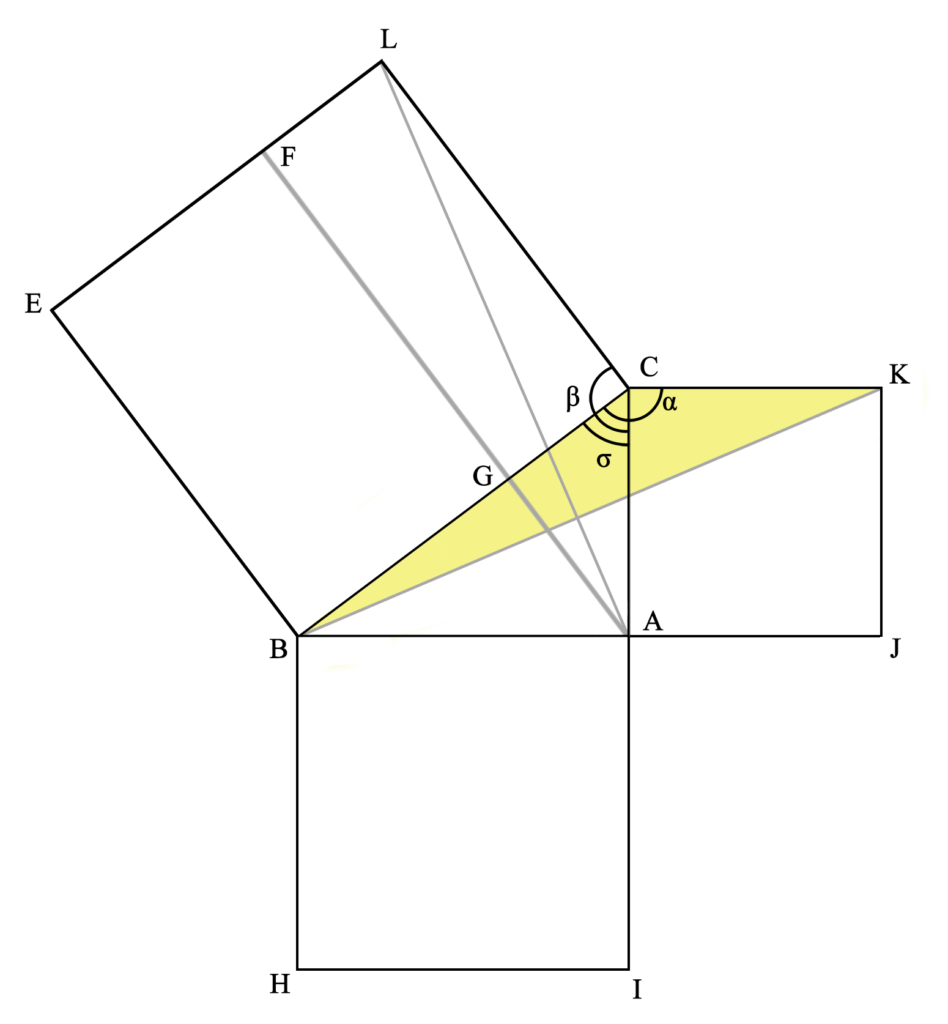
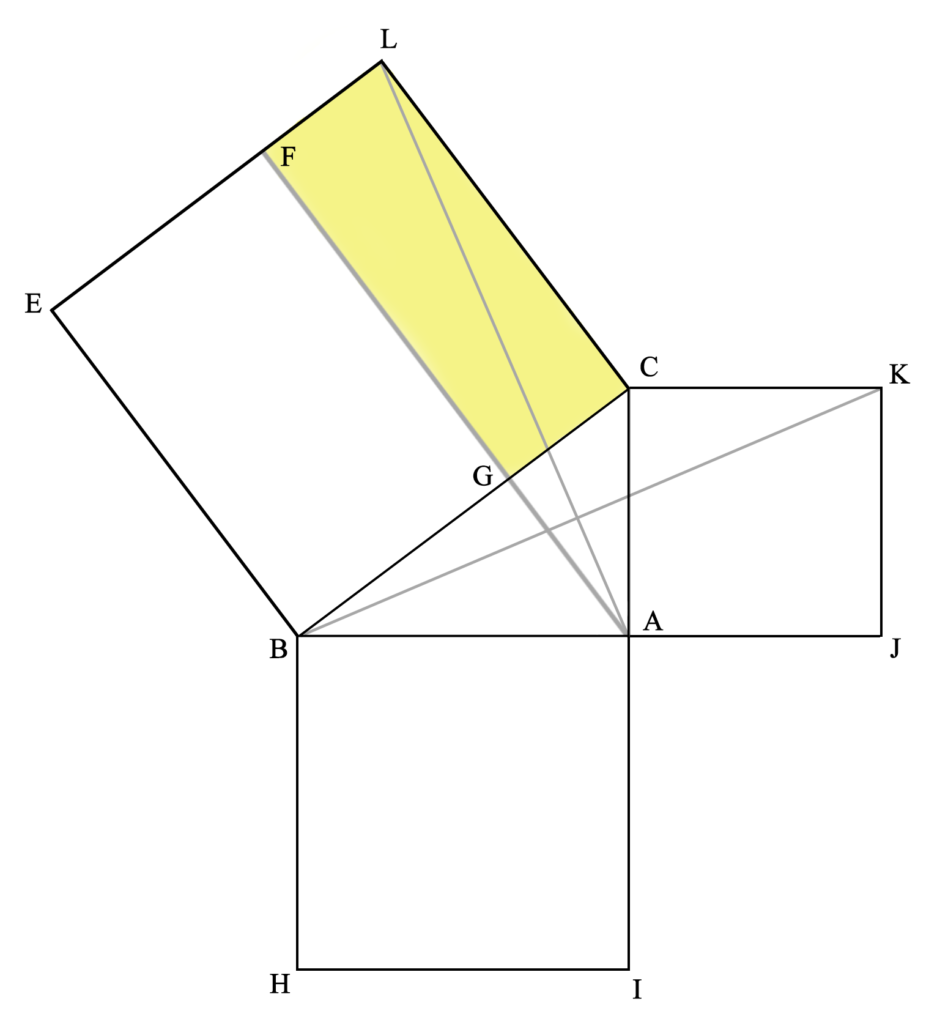
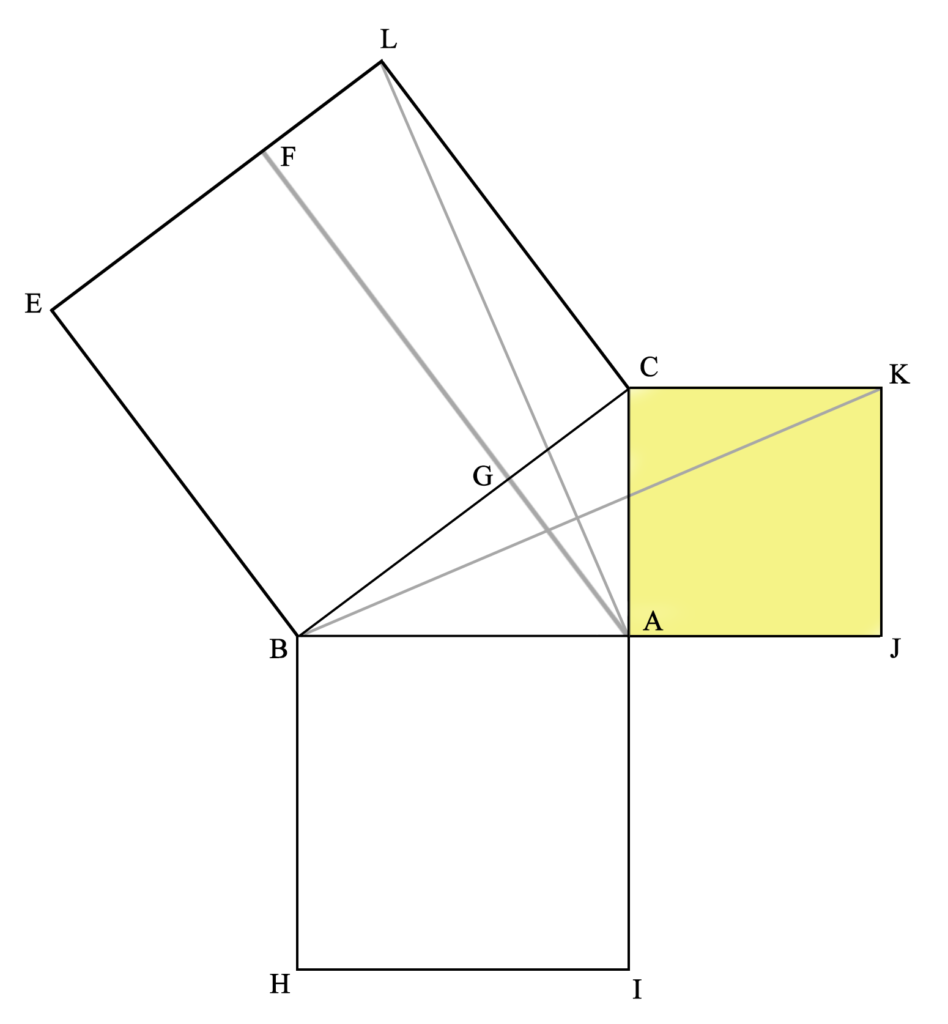
       Lo mismo se aplica con la otra parte del cuadrado formado sobre la hipotenusa (la coloreada aquí en amarillo). El triángulo ACL (idéntico al triángulo KBC, por ser el lado KC, igual a CA; el lado CL igual a CB; y por ser el ángulo α un recto más σ y β un recto más σ) es la mitad del cuadrilátero CLFG (por compartir la base CL y la altura LF, ya que las rectas LC y FA son paralelas), y el triángulo KBC es la mitad del cuadrado KCAJ (por compartir la base KC y la altura KJ, ya que las rectas KC y JB son paralelas).

       Y, así, obtenemos que (AC)²+(AB)²=(CB)². Y, como se concluye en geometría (post-griega): Q.E.D., quod erat demonstrandum [que era lo que había que demostrar].

Excurso para una demostración completa

       Sin embargo, definir el área de una figura por una fórmula tal como base x altura es propio del álgebra (la cual se fundamenta sobre la geometría, y no al revés). En la geometría griega esto se demuestra de la siguiente manera (acorde a la P41L1 de Euclides). Si dividimos el cuadrilátero GFEB por la mitad mediante una diagonal, uno de los triángulos que obtenemos (BFE o EGB) tiene la base BE y la altura FE, por lo que tendrá el mismo área que el triángulo AEB.

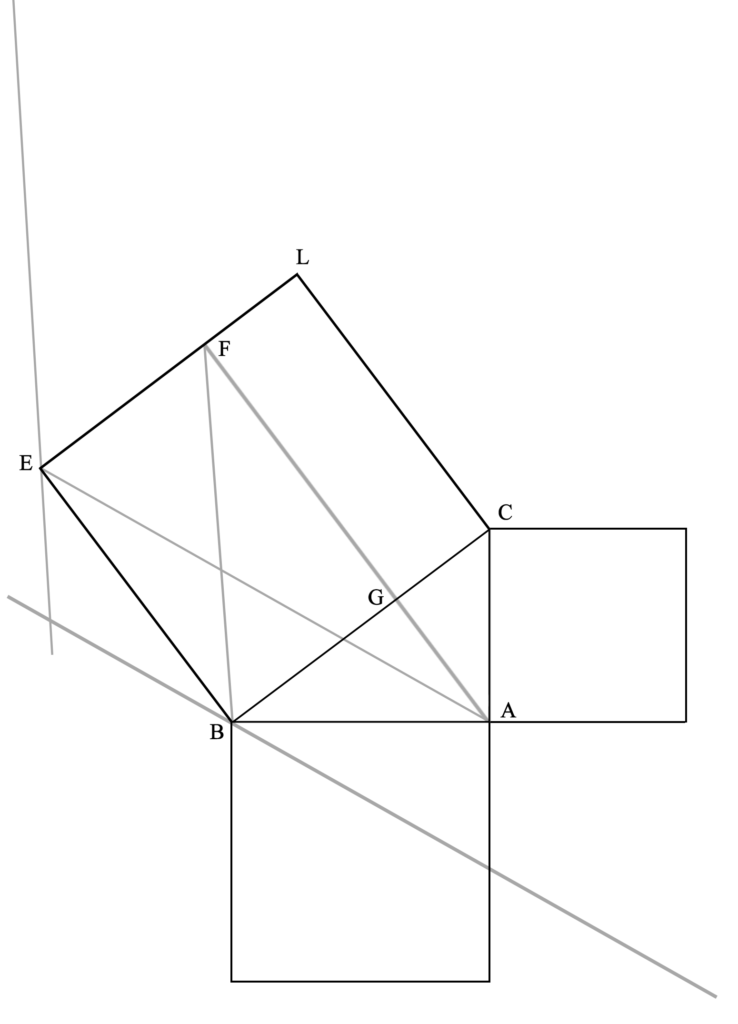
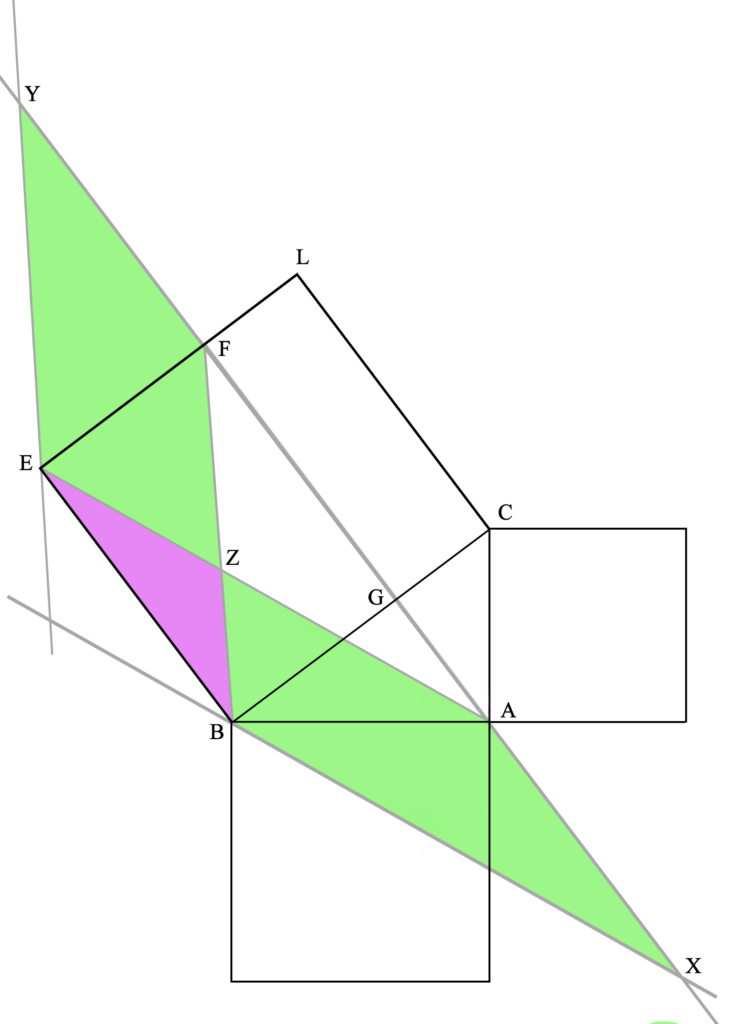
       Esto también se demuestra geométricamente, acorde a la P37L1 de Euclides. Para ello, dibujamos una paralela a AE por B y otra a BF por E (lo cual se puede hacer siguiendo los métodos ya demostrados por Euclides en P31L1). [Limpiamos la imagen anterior para visualizar fácilmente lo importante en este momento].

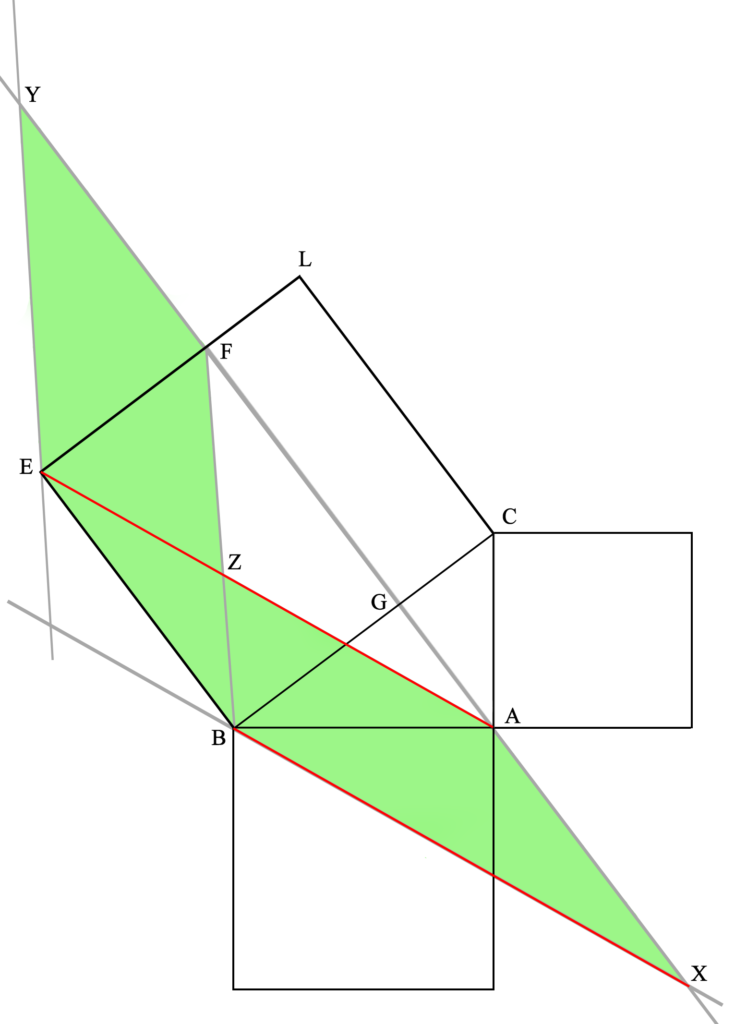
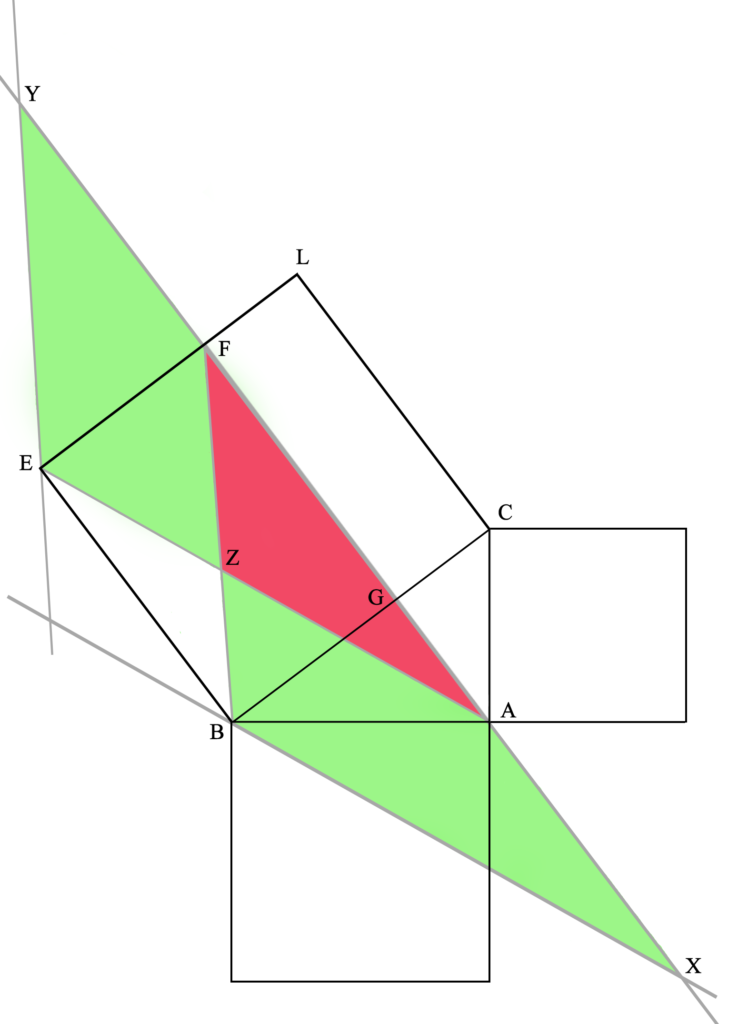
       Extendemos la línea GF hasta cortar las paralelas recién dibujadas en X e Y (este es uno de los procedimientos postulados –es decir, indemostrables pero permitidos– por Euclides [Postulado 2]).

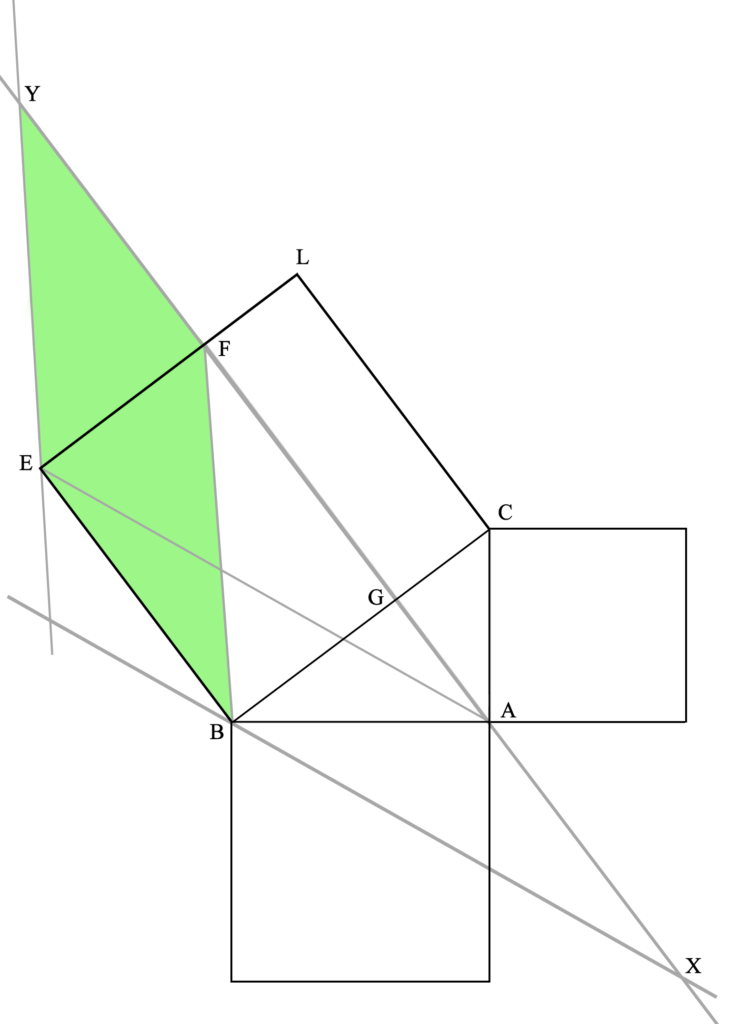
       En esta figura, los cuadriláteros XAEB y BFYE tienen la misma área.

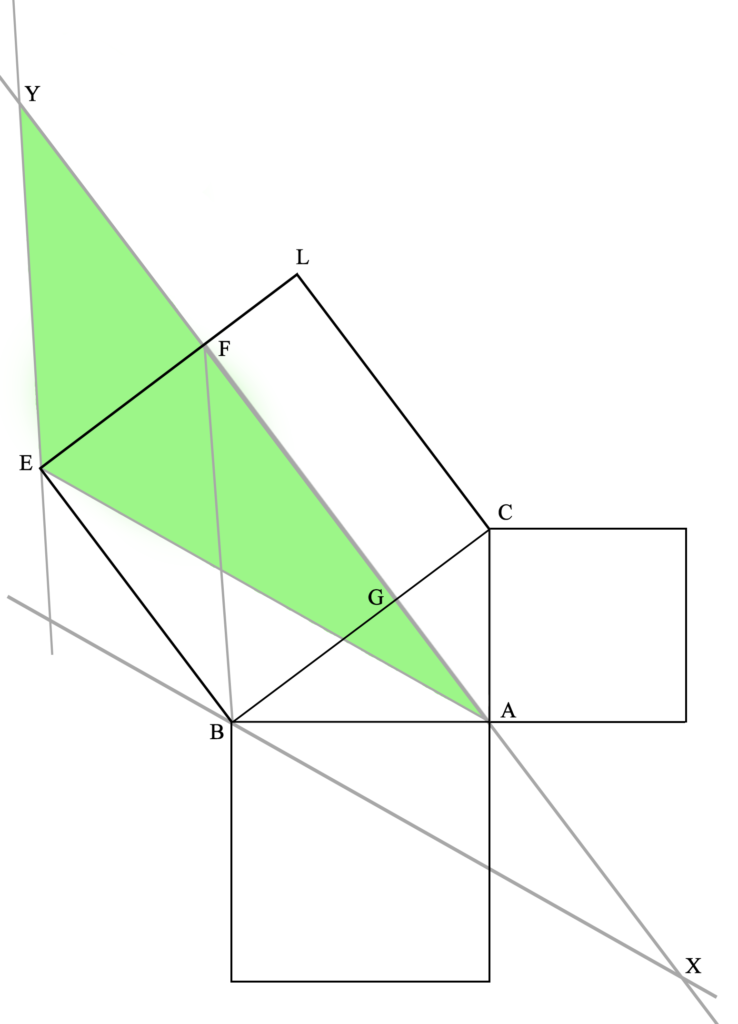
       Esto se demuestra (P35L1) viendo que los triángulos XBF y AEY son iguales.

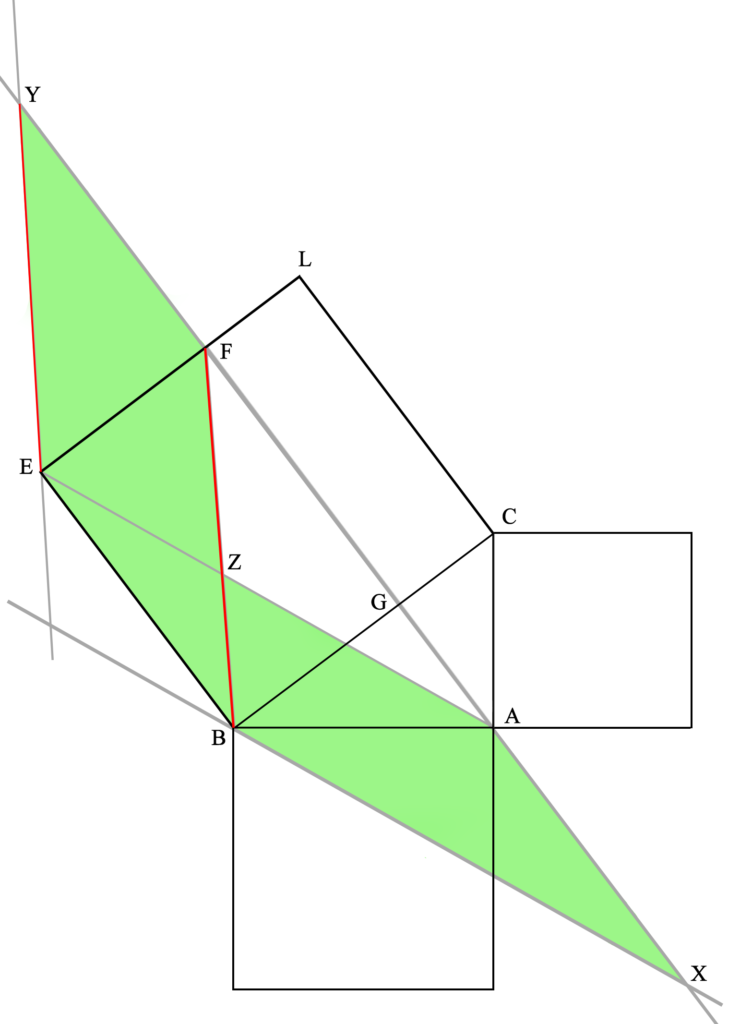
       Estos triángulos son iguales ya que, por un lado, las rectas XB y AE son iguales, por ser lados de un paralelogramo (lo cual es cierto por cómo hemos construido la figura). Téngase en cuenta que los paralelogramos se definen como aquellas figuras cuyos lados son paralelos dos a dos, por lo tanto, iguales dos a dos. Es decir, XB es igual a AE por definición del paralelogramo, pues los hemos construido como parte de una figura con estas características. Lo mismo ocurre con BF y EY.

       Y, además, los ángulos XBF y AEY (λ en ambos casos) son iguales.

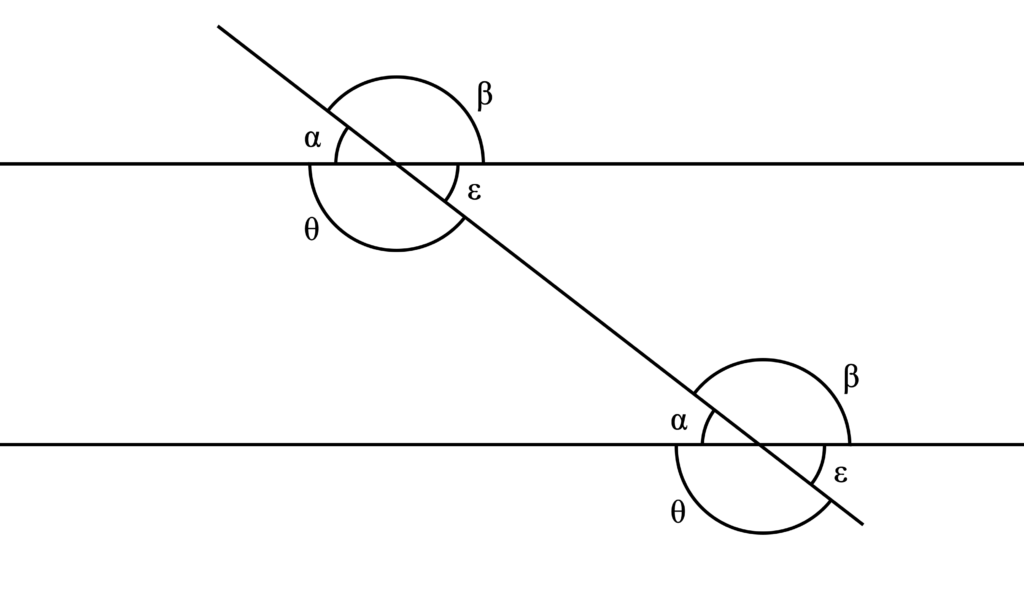
       Esto se demuestra (acorde a P29L1) en base a los ángulos de las líneas paralelas cortadas por otra recta cualquiera, lo cual Euclides demuestra por contradicción, ya que de no ser así (si los ángulos opuestos fueran distintos), las líneas se cortarían en algún punto y contradicen el quinto postulado. No obstante, también se puede probar que si

• θ+α=2⦝ (por definición)
• α+β=2⦝ (por definición)
• β+ε=2⦝ (por definición)
• θ+ε=2⦝ (por definición)
• ⸪ θ=β
• ⸪ α=ε

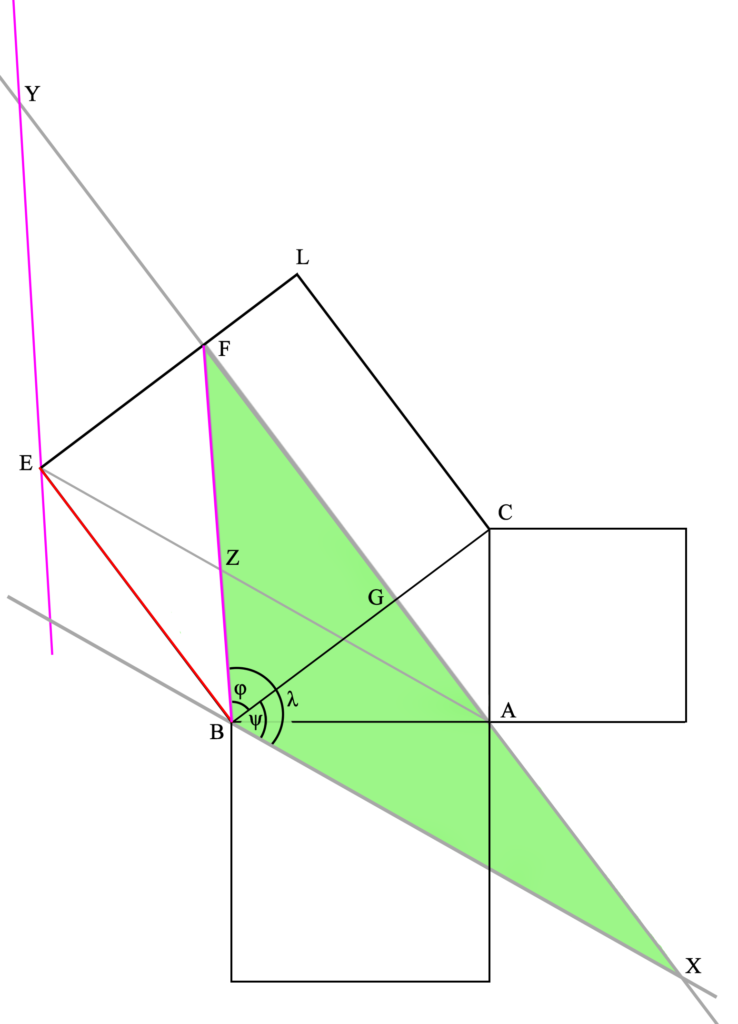
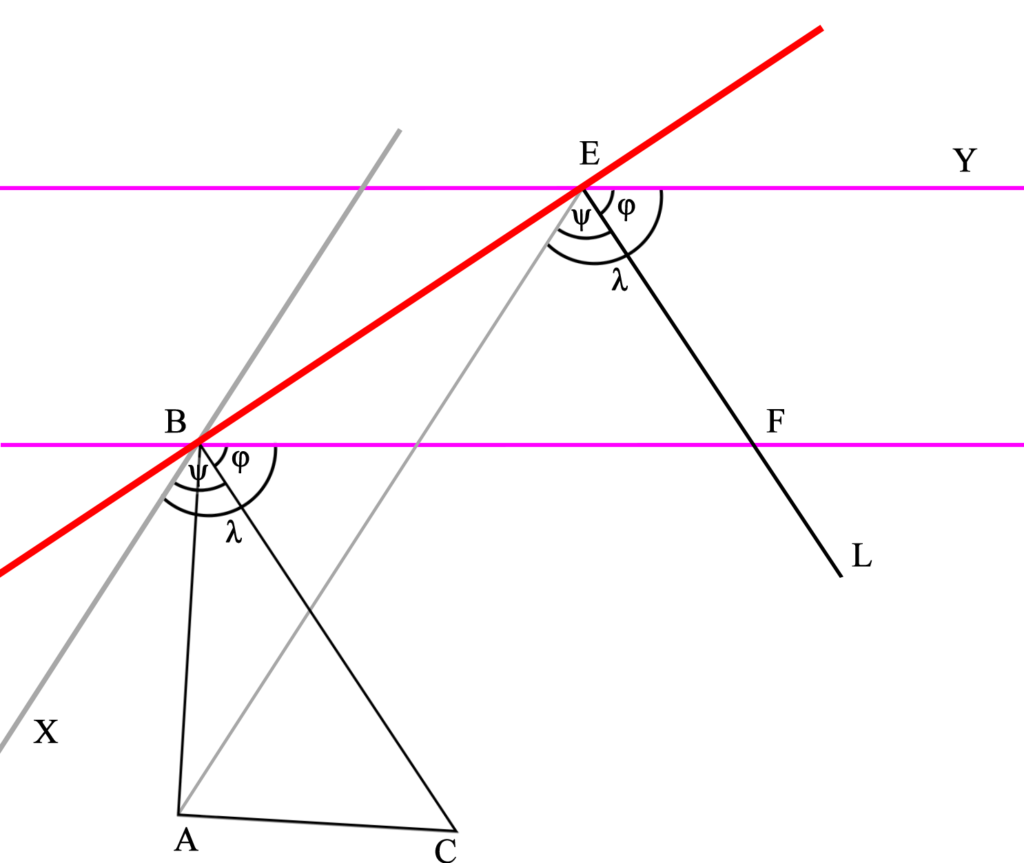
       En nuestro caso concreto, tenemos que λ es igual a φ+ψ, y φ_E es igual a φ_B, ya que BC y EL son paralelas que cortan a EY y BF (también paralelas entre sí). Lo mismo ocurre con ψ_E y ψ_B, ya que XB y AE (paralelas entre sí) también cortan a BC y EL.

       Por lo tanto, ambos triángulos tienen dos lados y un ángulo iguales, lo que significa que son iguales a todos los efectos (tanto en ángulos como en lados, por lo tanto también en área y perímetro). Esto se demuestra por superposición (P4L1), la que quizás sea la demostración más criticable de Euclides, pero es cierta en cualquier caso. Demostrada la igualdad entre los triángulos XBF y AEY, podemos demostrar que los cuadriláteros XAEB y BFYE son iguales si a ambos triángulos les quitamos el área AZF (permitida –es decir, propuesto como válido pero indemostrable– por noción común 3) y le sumamos el área BZE (permitido por noción común 2), y obtenemos los cuadriláteros mencionados anteriormente.

       Dado que estos dos cuadriláteros son iguales, y son respectivamente el doble en área de los triángulos BFE y AEB, estos dos triángulos serán iguales entre sí. Y aquí termina el excurso necesario para la demostración completa, pues esto era Q.E.D.

 

Citas

D: Diógenes Laercio. Vidas, opiniones y sentencias de los filósofos más ilustres. Pitágoras.

P: Porfirio. Vida de Pitágoras.

E: Euclides. Elementos. Proposición y Libro.